
【题目】定义在R上的函数![]() 满足
满足![]() ,且当
,且当![]() 时,
时,![]() ,对任意
,对任意![]() R,均有
R,均有![]() .
.
(1)求证:![]() ;
;
(2)求证:对任意![]() R,恒有
R,恒有![]() ;
;
(3)求证:![]() 是R上的增函数;
是R上的增函数;
(4)若![]() ,求
,求![]() 的取值范围.
的取值范围.
【答案】(1)见解析; (2)见解析; (3)见解析; (4)![]() .
.
【解析】
(1)利用赋值法,令a=b=0,求解f (0)的值即可;
(2)分类讨论x < 0和![]() 两种情况证明题中的不等式即可;
两种情况证明题中的不等式即可;
(3)由函数的性质可证得当![]() 时,f (x2) > f (x1),则f(x)是R上的增函数.
时,f (x2) > f (x1),则f(x)是R上的增函数.
(4)由题意结合函数的单调性和函数在特殊点的函数值可得x的取值范围是(0,3).
(1)证明:令a=b=0,得f (0)=f 2 (0),又因为f (0) ≠ 0,所以f (0)=1.
(2)当x < 0时,-x >0,
所以f (0) =f (x) f (-x) =1,即![]() ,
,
又因为![]() 时,
时,![]() ,所以对任意x∈R,恒有f (x) >0.
,所以对任意x∈R,恒有f (x) >0.
(3)证明:设![]() ,则
,则![]() ,所以f (x2)=f [(x2-x1)+x1]=f (x2-x1) f (x1).
,所以f (x2)=f [(x2-x1)+x1]=f (x2-x1) f (x1).
因为x2-x1>0,所以f (x2-x1)>1,又f (x1) > 0,
则f (x2-x1) f (x1) > f (x1),即f (x2) > f (x1),所以f(x)是R上的增函数.
(4)由f (x)·f (2x-x2) >1, f (0)=1得f (3x-x2) > f (0),
又由f (x) 为增函数,所以3x-x2 > 0 0 < x < 3.故x的取值范围是(0,3).


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:
【题目】已知AB是⊙O的直径,直线AF交⊙O于F(不与B重合),直线EC与⊙O相切于C,交AB于E,连接AC,且∠OAC=∠CAF,求证: 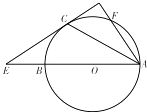
(1)AF⊥EC;
(2)若AE=5,AF=2,求AC.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() :
: ![]() 的离心率为
的离心率为![]() ,以原点为圆心,椭圆的短半轴长为半径的圆与直线
,以原点为圆心,椭圆的短半轴长为半径的圆与直线![]() 相切.
相切. ![]() 、
、![]() 是椭圆
是椭圆![]() 的右顶点与上顶点,直线
的右顶点与上顶点,直线![]() 与椭圆相交于
与椭圆相交于![]() 、
、![]() 两点.
两点.

(Ⅰ)求椭圆![]() 的方程;
的方程;
(Ⅱ)当四边形![]() 面积取最大值时,求
面积取最大值时,求![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设函数f(x)=ex(ax2﹣x﹣1)(a∈R).
(1)若函数f(x)在R上单调递减,求a的取值范围
(2)当a>0时,求f(|sinx|)的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知点A(0,-2),椭圆E: ![]() (a>b>0)的离心率为
(a>b>0)的离心率为![]() ,F是椭圆E的右焦点,直线AF的斜率为
,F是椭圆E的右焦点,直线AF的斜率为![]() ,O为坐标原点.
,O为坐标原点.
(1)求E的方程;
(2)设过点A的动直线l与E相交于P,Q两点.当△OPQ的面积最大时,求l的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在![]() 中,角A,B,C的对边分别为a,b,c,R表示
中,角A,B,C的对边分别为a,b,c,R表示![]() 的外接圆半径.
的外接圆半径.
(Ⅰ)如图,在以O圆心、半径为2的![]() O中,BC和BA是
O中,BC和BA是![]() O的弦,其中
O的弦,其中![]() ,求弦AB的长;
,求弦AB的长;
(Ⅱ)在![]() 中,若
中,若![]() 是钝角,求证:
是钝角,求证:![]() ;
;
(Ⅲ)给定三个正实数a、b、R,其中![]() ,问:a、b、R满足怎样的关系时,以a、b为边长,R为外接圆半径的
,问:a、b、R满足怎样的关系时,以a、b为边长,R为外接圆半径的![]() 不存在、存在一个或存在两个(全等的三角形算作同一个)?在
不存在、存在一个或存在两个(全等的三角形算作同一个)?在![]() 存在的情况下,用a、b、R表示c.
存在的情况下,用a、b、R表示c.

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设等差数列{an}的前n项的和为Sn , 已知a1=1, ![]() =12.
=12.
(1)求{an}的通项公式an;
(2)bn= ![]() ,bn的前n项和Tn , 求证;Tn<
,bn的前n项和Tn , 求证;Tn< ![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)的图像可以由y=cos2x的图像先纵坐标不变横坐标伸长到原来的2倍,再横坐标不变纵坐标伸长到原来的2倍,最后向右平移![]() 个单位而得到.
个单位而得到.
⑴求f(x)的解析式与最小正周期;
⑵求f(x)在x∈(0,π)上的值域与单调性.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=loga![]() (其中a>0,且a≠1).
(其中a>0,且a≠1).
(1)求函数f(x)的定义域;
(2)判断函数f(x)的奇偶性并给出证明;
(3)若x∈![]() 时,函数f(x)的值域是[0,1],求实数a的值.
时,函数f(x)的值域是[0,1],求实数a的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com