
【题目】如图,四棱锥![]() 中,
中,![]() 底面
底面![]() ,底面
,底面![]() 是直角梯形,
是直角梯形,![]() ,
,
![]() ,点
,点![]() 在
在![]() 上,且
上,且![]() .
.
(1)已知点![]() 在
在![]() ,且
,且![]() ,求证:平面
,求证:平面![]() 平面
平面![]() ;
;
(2)若![]() 的面积是梯形
的面积是梯形![]() 面积为
面积为![]() ,求点E到平面
,求点E到平面![]() 的距离.
的距离.

 愉快的寒假南京出版社系列答案
愉快的寒假南京出版社系列答案科目:高中数学 来源: 题型:
【题目】已知椭圆C的中心在坐标原点,焦点在x轴上,椭圆C上的点到焦点距离的最大值为3,离心率 ![]() .
.
(Ⅰ)求椭圆C的标准方程;
(Ⅱ)若经过左焦点F1且倾斜角为 ![]() 的直线l与椭圆交于A、B两点,求|AB|的值.
的直线l与椭圆交于A、B两点,求|AB|的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在空间几何体A﹣BCDE中,底面BCDE是梯形,且CD∥BE,CD=2BE=4,∠CDE=60°,△ADE是边长为2的等边三角形,F为AC的中点. (Ⅰ)求证:BF∥平面ADE;
(Ⅱ)若AC=4,求证:平面ADE⊥平面BCDE;
(Ⅲ)若AC=4,求几何体C﹣BDF的体积.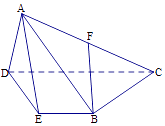
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】一汽车厂生产![]() 三类轿车,每类轿车均有舒适型和标准型两种型号,某月的产量如下表(单位:辆):
三类轿车,每类轿车均有舒适型和标准型两种型号,某月的产量如下表(单位:辆):
轿车 | 轿车 | 轿车 | |
舒适型 | 100 | 150 |
|
标准型 | 300 | 450 | 600 |
按类用分层抽样的方法在这个月生产的轿车中抽取50辆,其中有![]() 类轿车10辆.
类轿车10辆.
(I)求![]() 的值;
的值;
(II)用分层抽样的方法在![]() 类轿车中抽取一个容量为5的样本.将该样本看成一个总体,从中任取2辆,求至少有1辆舒适型轿车的概率;
类轿车中抽取一个容量为5的样本.将该样本看成一个总体,从中任取2辆,求至少有1辆舒适型轿车的概率;
(III)用随机抽样的方法从![]() 类舒适型轿车中抽取8辆,经检测它们的得分
类舒适型轿车中抽取8辆,经检测它们的得分![]() 的值如下:9.4,8.6,9.2,9.6,8.7,9.3,9.0,8.2,把这8辆轿车的得分看成一个总体,从中任取一个数
的值如下:9.4,8.6,9.2,9.6,8.7,9.3,9.0,8.2,把这8辆轿车的得分看成一个总体,从中任取一个数![]() ,设样本平均数为
,设样本平均数为![]() ,求
,求![]() 的概率.
的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知等差数列{an}的前n项和为 ![]() ,且a1与a5的等差中项为18.
,且a1与a5的等差中项为18.
(1)求{an}的通项公式;
(2)若an=2log2bn , 求数列{bn}的前n项和Tn .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】2017年春节期间,某服装超市举办了一次有奖促销活动,消费每超过600元(含600元),均可抽奖一次,抽奖方案有两种,顾客只能选择其中的一种.
方案一:从装有10个形状、大小完全相同的小球(其中红球3个,黑球7个)的抽奖盒中,一次性摸出3个球,其中奖规则为:若摸到3个红球,享受免单优惠;若摸出2个红球则打6折,若摸出1个红球,则打7折;若没摸出红球,则不打折.
方案二:从装有10个形状、大小完全相同的小球(其中红球3个,黑球7个)的抽奖盒中,有放回每次摸取1球,连摸3次,每摸到1次红球,立减200元.
(1)若两个顾客均分别消费了600元,且均选择抽奖方案一,试求两位顾客均享受免单优惠的概率;
(2)若某顾客消费恰好满1000元,试从概率的角度比较该顾客选择哪一种抽奖方案更合算?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com