
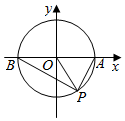
 如图,在平面直角坐标系xOy中,单位圆与x轴的正半轴与负半轴分别交于点A,B,角α的始边为OA,终边与单位圆交于x轴下方一点P.
如图,在平面直角坐标系xOy中,单位圆与x轴的正半轴与负半轴分别交于点A,B,角α的始边为OA,终边与单位圆交于x轴下方一点P.分析 (Ⅰ)若∠PBO=30°,先求出∠AOP=60°,即可写出与角α的终边相同的角β的集合;
(Ⅱ)若点P的横坐标为-$\frac{8}{17}$,得cosα的值,同时得sinα,即可求4sinα+cosα的值;
(Ⅲ)根据扇形的面积公式进行求解即可.
解答 解:(Ⅰ)若∠PBO=30°,
则∠BPO=30°,
∠BOP=180°-30°-30°=120°,
则∠AOP=60°,
则角α的终边相同的角β=-60°+k360°,
即{β|β=-60°+k360°,k∈Z};
(Ⅱ)若点P的横坐标为-$\frac{8}{17}$,
则cosα=-$\frac{8}{17}$,则sinα=$\sqrt{1-cos^2α}$=$\sqrt{1-(-\frac{8}{17})^{2}}$=$\frac{15}{17}$,
则4sinα+cosα=4×$\frac{15}{17}$-$\frac{8}{17}$=$\frac{52}{17}$;
(Ⅲ)若α=-$\frac{2π}{3}$,则∠AOP=$\frac{2π}{3}$,
则圆心角为钝角∠AOP的扇形面积S=$\frac{1}{2}$lr=$\frac{1}{2}$αr2=$\frac{1}{2}$×$\frac{2π}{3}$=$\frac{π}{3}$.
点评 本题主要考查三角函数的定义以及扇形的面积公式的计算,比较基础.


科目:高中数学 来源: 题型:选择题
| A. | 不存在一个平面α使得a?α,b?α | B. | 存在一个平面α使得a∥α,b∥α | ||
| C. | 不存在一个平面α使得a⊥α,b⊥α | D. | 存在一个平面α使得a∥α,b⊥α |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{48}$ | B. | $\frac{1}{24}$ | C. | $\frac{13}{24}$ | D. | $\frac{11}{24}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com