
【题目】已知函数![]() .
.
(Ⅰ)求![]() 的单调区间;
的单调区间;
(Ⅱ)若![]() ,若对任意
,若对任意![]() ,存在
,存在![]() ,使得
,使得![]() 成立,求实数
成立,求实数![]() 的取值范围.
的取值范围.
【答案】(1) ![]() 的单调递减区间是
的单调递减区间是![]() ,单调递增区间时
,单调递增区间时![]() ;(2)
;(2) ![]() .
.
【解析】试题分析:(1)求导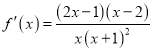 ,由
,由![]() 得减区间,由
得减区间,由![]() 得增区间;
得增区间;
(2)当![]() 时,
时, ![]() ,又
,又![]() ,所以对任意
,所以对任意![]() ,存在
,存在![]() ,使得
,使得![]() 成立,
成立, ![]() 存在
存在![]() ,使得
,使得![]() 成立,
成立, ![]() 存在
存在![]() ,使得
,使得![]() 成立,
成立, ![]() 的图象与直线
的图象与直线![]() 有交点,
有交点, ![]() 方程
方程![]() 在
在![]() 上有解.
上有解.
试题解析:
(Ⅰ)因为![]() ,
,
所以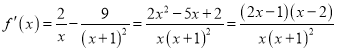 ,
,
因为![]() 的定义域为
的定义域为![]() ,当
,当![]() 时
时![]() ,
, ![]() 或
或![]() 时
时![]() ,
,
所以![]() 的单调递减区间是
的单调递减区间是![]() ,单调递增区间时
,单调递增区间时![]() .
.
(Ⅱ)由(Ⅰ)知, ![]() 在
在![]() 上单调递减,在
上单调递减,在![]() 上单调递增,所以当
上单调递增,所以当![]() 时
时![]() ,
,
又![]() ,
,
所以对任意![]() ,存在
,存在![]() ,使得
,使得![]() 成立,
成立,
![]() 存在
存在![]() ,使得
,使得![]() 成立,
成立,
![]() 存在
存在![]() ,使得
,使得![]() 成立,
成立,
因为![]() 表示点
表示点![]() 与点
与点![]() 之间距离的平方,
之间距离的平方,
所以存在![]() ,使得
,使得![]() 成立,
成立,
![]() 的图象与直线
的图象与直线![]() 有交点,
有交点,
![]() 方程
方程![]() 在
在![]() 上有解,
上有解,
设![]() ,则
,则![]() ,
,
当![]() 时,
时, ![]() 单调递增,当
单调递增,当![]() 时,
时, ![]() 单调递减,
单调递减,
又![]() ,所以
,所以![]() 的值域是
的值域是![]() ,
,
所以实数![]() 的取值范围是
的取值范围是![]() .
.


 浙江名校名师金卷系列答案
浙江名校名师金卷系列答案科目:高中数学 来源: 题型:
【题目】已知椭圆 ![]() 的一个焦点与抛物线y2=8x的焦点重合,点
的一个焦点与抛物线y2=8x的焦点重合,点 ![]() 在C上.
在C上.
(1)求椭圆C的方程;
(2)若椭圆C的一条弦被M(2,1)点平分,求这条弦所在的直线方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设数列{an}满足:a1=1,an+1=3an , n∈N* . 设Sn为数列{bn}的前n项和,已知b1≠0,2bn﹣b1=S1Sn , n∈N*(Ⅰ)求数列{an},{bn}的通项公式;
(Ⅱ)设cn=bnlog3an , 求数列{cn}的前n项和Tn .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,四棱锥P﹣ABCD中,底面ABCD为菱形,PA⊥底面ABCD, ![]() ,PA=2,E是PC上的一点,PE=2EC.
,PA=2,E是PC上的一点,PE=2EC.
(Ⅰ)证明:PC⊥平面BED;
(Ⅱ)设二面角A﹣PB﹣C为90°,求PD与平面PBC所成角的大小.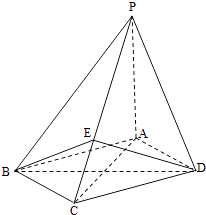
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知{an}是公差为3的等差数列,数列{bn}满足b1=1,b2= ![]() ,anbn+1+bn+1=nbn .
,anbn+1+bn+1=nbn .
(Ⅰ)求{an}的通项公式;
(Ⅱ)求{bn}的前n项和.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com