
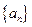 中,已知
中,已知
 .
.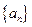 的通项公式;
的通项公式;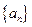 的前
的前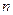 项和
项和
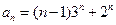
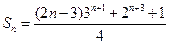
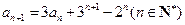
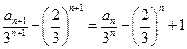 ,------------------3分
,------------------3分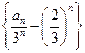 是首项为
是首项为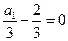 ,公差为1等差数列,
,公差为1等差数列,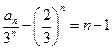 , ---------------------------------------------------6分
, ---------------------------------------------------6分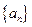 的通项公式为
的通项公式为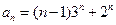 ------------------------7分
------------------------7分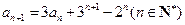
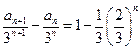 -----------------------------
----------------------------- -------------------2分
-------------------2分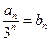 ,则
,则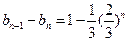 ---------------------------------------3分
---------------------------------------3分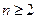 时
时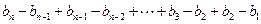
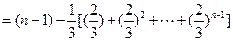 --5分
--5分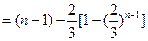
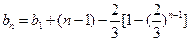
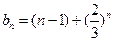 -----------------------------------------------------------6分
-----------------------------------------------------------6分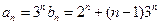 ------------------------------------------------7分
------------------------------------------------7分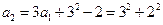 ,--------------------------------1分
,--------------------------------1分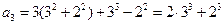 ,---------------------------------2分
,---------------------------------2分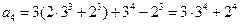 .------------------------3分
.------------------------3分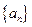 的通项公式为
的通项公式为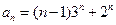 ------------4分
------------4分 用数学归纳法证明.
用数学归纳法证明.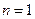 时,
时,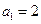 ,等式成立.
,等式成立.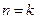 (
(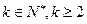 )时等式成立,即
)时等式成立,即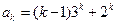 ,
,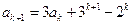
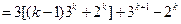
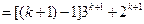 .----------------------------------------6分
.----------------------------------------6分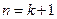 时等式也成立.根据①和②可知,
时等式也成立.根据①和②可知,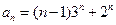 对任何
对任何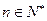 都成立.------------------------7分
都成立.------------------------7分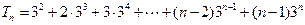 ,----------①---------8分
,----------①---------8分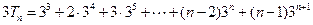 ------------②------9分
------------②------9分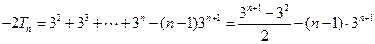 ,----------10分
,----------10分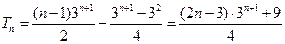 .-
.- ------------12分
------------12分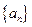 的前
的前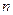 项和
项和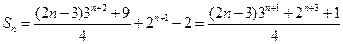 . ---14分
. ---14分

科目:高中数学 来源:不详 题型:解答题
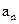 ﹜中,
﹜中, =
=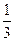 ,前n项和
,前n项和 满足
满足 +1-
+1- =(
=(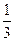 )n+1 (n
)n+1 (n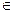 N*
N* )
)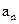 ﹜的通项公式
﹜的通项公式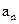 以及前n项和
以及前n项和
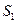 ,t(
,t(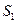 +
+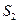 ), 3(
), 3(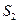 +
+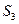 )成等差数列,求实数t的值。
)成等差数列,求实数t的值。查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
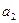 ,
,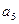 是方程
是方程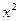
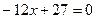 的两根, 数列
的两根, 数列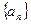 是公差为正的等差数列,数列
是公差为正的等差数列,数列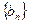 的前
的前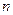 项和为
项和为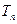 ,且
,且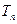
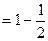
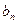
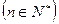 .
.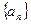 ,
,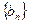 的通项公式; (2)记
的通项公式; (2)记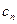 =
=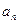
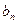 ,求数列
,求数列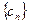 的前
的前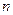 项和
项和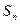 .
.查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
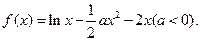
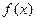 在定义域内单调递增,求
在定义域内单调递增,求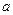 的取值范围;
的取值范围;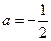 且关于x的方程
且关于x的方程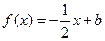 在
在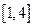 上恰有两个不相等的实数根,求实数
上恰有两个不相等的实数根,求实数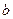 的取值范围;
的取值范围;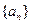 满足:
满足: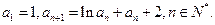 求证:
求证: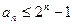
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com