
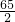 ,且角B为钝角,求BC边的长;
,且角B为钝角,求BC边的长;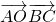 的值.
的值.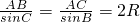 ,把AB=25,AC=39,外接圆O的半径为
,把AB=25,AC=39,外接圆O的半径为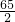 ,且角B为钝角代入求得sinB=
,且角B为钝角代入求得sinB= ,sinC=
,sinC= ,
, ,cosB=-
,cosB=- ,∴sin(B+C)=sinBcosC+cosBsinC=
,∴sin(B+C)=sinBcosC+cosBsinC= .
.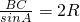 ,∴BC=2RsinA=65sin(B+C)=16.
,∴BC=2RsinA=65sin(B+C)=16.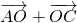 =
= ,∴
,∴ +
+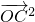 +2
+2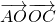 =
= =392,
=392,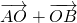 =
= ,∴
,∴ +
+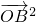 +2
+2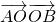 =
= =252,
=252,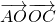 -2
-2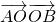 =896,
=896,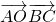 =896,∴
=896,∴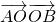 =448.
=448. ,sinC=
,sinC= ,从而求得 cosC=
,从而求得 cosC= ,cosB=-
,cosB=- .再利用两角和的正弦公式求得 sin(B+C) 的值,利用正弦定理求得BC的值.
.再利用两角和的正弦公式求得 sin(B+C) 的值,利用正弦定理求得BC的值.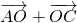 =
= 平方,再把
平方,再把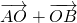 =
= 平方,相减可得 2
平方,相减可得 2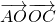 -2
-2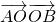 =896,即 2
=896,即 2 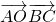 =896,从而求得
=896,从而求得 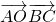 的值.
的值.

科目:高中数学 来源: 题型:
| 65 |
| 2 |
| AO |
| BC |
查看答案和解析>>
科目:高中数学 来源: 题型:
| 65 |
| 2 |
| AO |
| BC |
查看答案和解析>>
科目:高中数学 来源:2012-2013学年湖北省荆州市江陵县实验高中高三(上)期中数学试卷(理科)(解析版) 题型:解答题
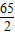 ,且角B为钝角,求BC边的长;
,且角B为钝角,求BC边的长;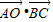 的值.
的值.查看答案和解析>>
科目:高中数学 来源:2012-2013学年山东省青岛二中高三(上)11月月考数学试卷(理科)(解析版) 题型:解答题
 ,且角B为钝角,求BC边的长;
,且角B为钝角,求BC边的长;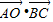 的值.
的值.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com