
| A. | $(\;\frac{5}{4}\;,\;6\;)$ | B. | $(\;\frac{5}{3}\;,\;6\;)$ | C. | $(\;\frac{7}{5}\;,\;5\;)$ | D. | $(\;\frac{5}{4}\;,\;5\;)$ |
分析 当m=2时,f(a)=f(b)=f(c)=1,是等边三角形的三边长;当m>2时,只要$2(1+\frac{m-2}{3})>m-1$即可,当m<2时,只要$1+\frac{m-2}{3}<2(m-1)$即可,由此能求出结果.
解答 解:当m=2时,f(x)=$\frac{cosx+2}{cosx+2}$=1,
此时f(a)=f(b)=f(c)=1,是等边三角形的三边长,成立;
当m>2时,$f(x)∈[1+\frac{m-2}{3},m-1]$,
只要$2(1+\frac{m-2}{3})>m-1$即可,解得2<m<5;
当m<2时,$f(x)∈[m-1,1+\frac{m-2}{3}]$,
只要$1+\frac{m-2}{3}<2(m-1)$即可,
解得$\frac{7}{5}<m<2$,
综上$m∈(\frac{7}{5},5)$.
故选:C.
点评 本题考查实数的取值范围的求法,是基础题,解题时要认真审题,注意分类讨论思想的合理运用.


 步步高达标卷系列答案
步步高达标卷系列答案科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | {x|1<x<3} | B. | {x|-1<x<3} | C. | {x|-1<x<0或0<x<3} | D. | {x|-1<x<0或1<x<3} |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
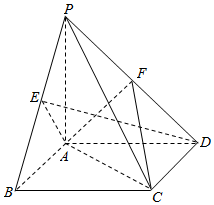 在四棱锥P-ABCD中,底面ABCD为正方形,PA⊥平面ABCD,PA=AB=2,E,F分别是PB,PD的中点.
在四棱锥P-ABCD中,底面ABCD为正方形,PA⊥平面ABCD,PA=AB=2,E,F分别是PB,PD的中点.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com