
分析 设g(x)=x2-2ax+3,由f(x)=log$\frac{1}{2}$(x2-2ax+3)的值域为R,知g(x)=x2-2ax+3可以取所有的正值,图象不能够在x轴上方.△≥0即可.
解答 解:设g(x)=x2-2ax+3,由f(x)=log$\frac{1}{2}$(x2-2ax+3)的值域为R,
根据对数函数的图象性质得出:g(x)=x2-2ax+3可以取所有的正值,
图象不能够在x轴上方
∴△=4a2-12≥0,
即a$≥\sqrt{3}$或a$≤-\sqrt{3}$
故答案为:a$≥\sqrt{3}$或a$≤-\sqrt{3}$
点评 本题主要考查了由二次函数与对数函数复合的复合函数,解题的关键是要熟悉对数函数的性质,解题时容易误认为△<0,要注意区别与函数的定义域为R的限制条件


 名师导航单元期末冲刺100分系列答案
名师导航单元期末冲刺100分系列答案 名校名卷单元同步训练测试题系列答案
名校名卷单元同步训练测试题系列答案科目:高中数学 来源: 题型:选择题
| A. | 10 | B. | 19 | C. | -1 | D. | -10 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
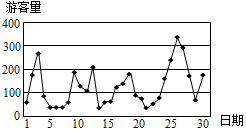 已知国家某5A级大型景区对拥挤等级与每日游客数量n(单位:百人)的关系有如下规定:当n∈[0,100)时,拥挤等级为“优”;当n∈[100,200)时,拥挤等级为“良”;当n∈[200,300)时,拥挤等级为“拥挤”;当n≥300时,拥挤等级为“严重拥挤”.该景区对6月份的游客数量作出如图的统计数据:
已知国家某5A级大型景区对拥挤等级与每日游客数量n(单位:百人)的关系有如下规定:当n∈[0,100)时,拥挤等级为“优”;当n∈[100,200)时,拥挤等级为“良”;当n∈[200,300)时,拥挤等级为“拥挤”;当n≥300时,拥挤等级为“严重拥挤”.该景区对6月份的游客数量作出如图的统计数据:| 游客数量 (单位:百人) | [0,100) | [100,200) | [200,300) | [300,400] |
| 天数 | a | 10 | 4 | 1 |
| 频率 | b | $\frac{1}{3}$ | $\frac{2}{15}$ | $\frac{1}{30}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com