
分析 函数f(x)=ax2+bx,且1≤f(1)≤2,2≤f(-2)≤4.可得:$\left\{\begin{array}{l}{1≤a+b≤2}\\{1≤2a-b≤2}\end{array}\right.$,如图所示,表示的可行域为四边形BACD及其内部的点,可得A,B,C,D.
向量$\overrightarrow m$=(a,b),$\overrightarrow n$=(0,2),$\overrightarrow m$-$\overrightarrow n$=(a,b-2),设点P(0,2),可得|$\overrightarrow m$-$\overrightarrow n$|=$\sqrt{{a}^{2}+(b-2)^{2}}$∈[|PC|,|PA|].
解答 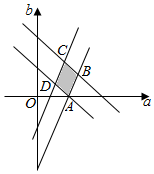 解:函数f(x)=ax2+bx,且1≤f(1)≤2,2≤f(-2)≤4.
解:函数f(x)=ax2+bx,且1≤f(1)≤2,2≤f(-2)≤4.
∴$\left\{\begin{array}{l}{1≤a+b≤2}\\{2≤4a-2b≤4}\end{array}\right.$,即$\left\{\begin{array}{l}{1≤a+b≤2}\\{1≤2a-b≤2}\end{array}\right.$,
如图所示,表示的可行域为四边形BACD及其内部的点,可得A(1,0),B$(\frac{4}{3},\frac{2}{3})$,C(1,1),D$(\frac{2}{3},\frac{1}{3})$.
向量$\overrightarrow m$=(a,b),$\overrightarrow n$=(0,2),$\overrightarrow m$-$\overrightarrow n$=(a,b-2),
设点P(0,2),
|PC|=$\sqrt{2}$,|PB|=$\frac{4\sqrt{2}}{3}$,|PA|=$\sqrt{5}$,|PD|=$\frac{\sqrt{29}}{3}$.
则|$\overrightarrow m$-$\overrightarrow n$|=$\sqrt{{a}^{2}+(b-2)^{2}}$∈[|PC|,|PA|]=$[\sqrt{2},\sqrt{5}]$,
故答案为:$[\sqrt{2},\sqrt{5}]$.
点评 本题考查了线性规划的有关知识、不等式的性质、两点之间的距离公式,考查了数形结合方法、推理能力与计算能力,属于中档题.


 每课必练系列答案
每课必练系列答案 巧学巧练系列答案
巧学巧练系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{\sqrt{6}}{6}$ | B. | -$\frac{\sqrt{6}}{6}$ | C. | 1 | D. | -1 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (0,$\frac{1}{8}$] | B. | (0,$\frac{1}{4}$]∪[$\frac{5}{8}$,1) | C. | (0,$\frac{5}{8}$] | D. | (0,$\frac{1}{8}$]∪[$\frac{1}{4}$,$\frac{5}{8}$] |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 下面是某港口一天中部分时刻测量得到的水深表(时间单位:小时,水深单位:米)
下面是某港口一天中部分时刻测量得到的水深表(时间单位:小时,水深单位:米) | 时刻 | 0:00 | 3:00 | 6:00 | 9:00 | 12:00 | 15:00 | 18:00 | 21:00 | 24:00 |
| 水深 | 6.5 | 8.5 | 6.5 | 4.5 | 6.5 | 8.5 | 6.5 | 4.5 | 6.5 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com