
分析 分别求出△BDF、五边形ABCDE的面积,一面积为测度,即可得出结论.
解答 解:由题意,ABDF为长方形,设AB=1,则BD=$\sqrt{3}$,S△BDF=$\frac{1}{2}×\sqrt{3}×1$=$\frac{\sqrt{3}}{2}$,
五边形ABCDE的面积S=1×$\sqrt{3}$+$\frac{1}{2}×1×1×\frac{\sqrt{3}}{2}$=$\frac{5\sqrt{3}}{4}$,
∴往五边形ABCDE内投掷一点,该点落在△BDF内的概率为$\frac{\frac{\sqrt{3}}{2}}{\frac{5\sqrt{3}}{4}}$=$\frac{2}{5}$,
故答案为$\frac{2}{5}$.
点评 此题考查了几何概率的求法,利用面积比计算出几何概率,根据题意求出五边形的面积比是解本题的关键.


科目:高中数学 来源: 题型:选择题
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
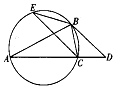 如图,已知△ABC内接于圆,AB=AC,过点B作此圆的切线,与AC的延长线交于点D,且BD=2CD.
如图,已知△ABC内接于圆,AB=AC,过点B作此圆的切线,与AC的延长线交于点D,且BD=2CD.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (-∞,-2)∪(2,+∞) | B. | $[-2\sqrt{3},-2)∪(2,2\sqrt{3}]$ | C. | $[2,2\sqrt{3})$ | D. | [2,+∞) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $[\frac{3}{2},3)$ | B. | (3,+∞) | C. | $(1,\frac{3}{2})$ | D. | ($\frac{3}{2}$,3) |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com