
分析 (1)求出函数的导数,通过讨论a的范围,判断函数的单调性即可;
(2)结合(1)通过讨论a的范围,判断出函数的单调性,从而确定a的范围即可;
(3)取a=2,得到在(0,+∞)上,ln(x+1)>$\frac{2x}{x+2}$,令x=$\frac{1}{n}$,作和即可证出结论.
解答 解:(1)f′(x)=$\frac{1}{x+1}$-$\frac{2a}{{{{(x+2)}^2}}}$=$\frac{{{x^2}+(4-2a)x+(4-2a)}}{{(x+1){{(x+2)}^2}}}$,x>-1,
其中x2+(4-2a)x+4-2a=0的△=4a(a-2).
当△≤0即a∈[0,2]时,f′(x)≥0恒成立,则f(x)在(-1,+∞)上单调递增;
当a<0时,f′(x)>0,则f(x)在(-1,+∞)上单调递增;
当a>2时,方程x2+(4-2a)x+4-2a=0有两根为a-2-$\sqrt{{a^2}-2a}$,a-2+$\sqrt{{a^2}-2a}$,
∵-1=a-2-$\sqrt{{(a-1)}^{2}}$<a-2-$\sqrt{{a^2}-2a}$<0,a-2+$\sqrt{{a^2}-2a}$>0,
∴当a>2时,f(x)在(-1,a-2-$\sqrt{{a^2}-2a}$)与(a-2+$\sqrt{{a^2}-2a}$,+∞)上递增,
在(a-2-$\sqrt{{a^2}-2a}$,a-2+$\sqrt{{a^2}-2a}$)上递减;
当a≤2时,f(x)在(-1,+∞)上单调递增.(5分)
(2)当a≤2时,f(x)在(0,+∞)上单调递增,f(x)>f(0)=0满足条件,
当a>2时,f(x)在(0,a-2+$\sqrt{{a^2}-2a}$)上递减,此时f(x)<f(0)=0不满足条件,
故a∈(-∞,2].(8分)
(3)若a=2时,在(0,+∞)上,ln(x+1)>$\frac{2x}{x+2}$,
令x=$\frac{1}{n}$,则ln$\frac{n+1}{n}$>$\frac{2}{2n+1}$,ln$\frac{n}{n-1}$>$\frac{2}{2n-1}$,…,ln$\frac{3}{2}$>$\frac{2}{5}$,ln2>$\frac{2}{3}$,
∴ln$\frac{n+1}{n}$+ln$\frac{n}{n-1}$+…+ln$\frac{3}{2}$+ln2=ln(n+1)>$\frac{2}{2n+1}$+$\frac{2}{2n-1}$+…+$\frac{2}{5}$+$\frac{2}{3}$,
即n+1>${e^{\frac{2}{3}+\frac{2}{5}+…+\frac{2}{2n+1}}}$.(12分)
点评 本题考查了函数的单调性问题,考查导数的应用以及不等式的证明,考查分类讨论思想,是一道综合题.


 优生乐园系列答案
优生乐园系列答案科目:高中数学 来源: 题型:选择题
| A. | [-2,0)∪(0,2] | B. | [-2,0)∪[2,+∞) | C. | (-∞,2]∪(0,2] | D. | (-∞,-2]∪[2,+∞) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{4}$ | B. | $\frac{1}{18}$ | C. | $\frac{1}{6}$ | D. | $\frac{1}{12}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
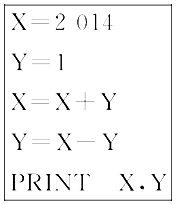
| A. | 2 015,2 013 | B. | 2 013,2 015 | C. | 2 015,2 015 | D. | 2 015,2 014 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图,在四棱锥P-ABCD中,PA⊥CD,AD∥BC,∠ADC=∠PAB=90°,BC=CD=AE=$\frac{1}{2}$AD=1,PA=2.
如图,在四棱锥P-ABCD中,PA⊥CD,AD∥BC,∠ADC=∠PAB=90°,BC=CD=AE=$\frac{1}{2}$AD=1,PA=2.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 1 | B. | $\frac{6}{5}$ | C. | $\frac{3}{2}$ | D. | 2 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com