
 ,|BC|=4,|AC|=1,动点M满足
,|BC|=4,|AC|=1,动点M满足 =λ
=λ +μ
+μ ,且λμ=
,且λμ= .
.
 |最小值,并指出此时
|最小值,并指出此时 与
与 ,
, 的夹角;
的夹角; |-|
|-| ||恒为常数k?若存在,指出常数k的值,若不存在,说明理由.
||恒为常数k?若存在,指出常数k的值,若不存在,说明理由. 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源:不详 题型:解答题
 ,求证:a∥b.
,求证:a∥b.查看答案和解析>>
科目:高中数学 来源:不详 题型:填空题
查看答案和解析>>
科目:高中数学 来源:不详 题型:填空题
 ,∠AOB为锐角,OM平分∠AOB,点N为线段AB的中点,
,∠AOB为锐角,OM平分∠AOB,点N为线段AB的中点, ,若点P在阴影部分(含边界)内,则在下列给出的关于x、y的式子中,满足题设条件的为 (写出所有正确式子的序号).
,若点P在阴影部分(含边界)内,则在下列给出的关于x、y的式子中,满足题设条件的为 (写出所有正确式子的序号).
查看答案和解析>>
科目:高中数学 来源:不详 题型:单选题
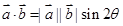 ,(其中
,(其中 为
为 、
、 的夹角),已知△ABC中,
的夹角),已知△ABC中,
 ,则此三角形一定是( )
,则此三角形一定是( )| A.等腰三角形 | B.直角三角形 | C.锐角三角形 | D.钝角三角形 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com