
(1)化简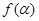 =
=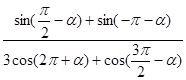 ; (2)若
; (2)若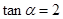 ,求
,求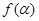 的值.
的值.
科目:高中数学 来源: 题型:解答题
(2014·济南模拟)已知函数f(x)=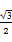 sinωx-sin2
sinωx-sin2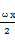 +
+ (ω>0)的最小正周期为π.
(ω>0)的最小正周期为π.
(1)求ω的值及函数f(x)的单调递增区间.
(2)当x∈ 时,求函数f(x)的取值范围.
时,求函数f(x)的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com