
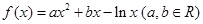
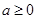 ,求
,求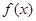 的单调区间;
的单调区间;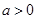 ,且对于任意
,且对于任意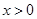 ,
,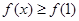 .试比较
.试比较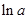 与
与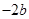 的大小.
的大小.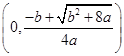 ,单调递增区间是
,单调递增区间是

 得
得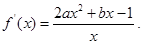
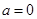 时,
时,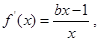
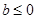 ,当
,当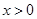 时,
时,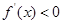 恒成立,
恒成立,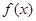 的单调递减区间是
的单调递减区间是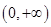 .
.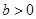 ,当
,当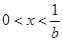 时,
时,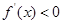 ,函数
,函数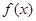 单调递减,
单调递减,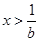 时,
时,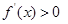 ,函数
,函数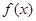 单调递增.
单调递增.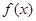 的单调递减区间是
的单调递减区间是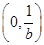 ,单调递增区间是
,单调递增区间是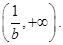
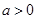 时,令
时,令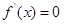 得
得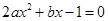 ,
,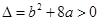 得
得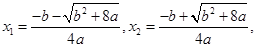
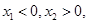
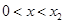 时,
时,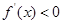 ,函数
,函数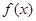 单调递减;
单调递减;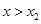 时,
时,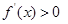 ,函数
,函数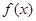 单调递增.
单调递增.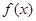 的单调递减区间是
的单调递减区间是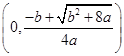 ,
, .
.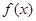 在
在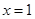 处取得最小值,
处取得最小值,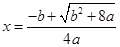 是
是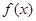 的唯一极小值点,
的唯一极小值点,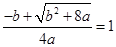 ,整理得
,整理得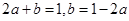 ,
,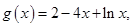 则
则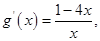
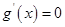 得
得
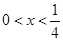 时,
时,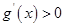 ,
,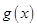 单调递增;
单调递增;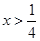 时,
时,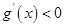 ,
,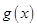 单调递减.
单调递减.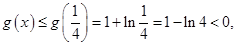
 ,即
,即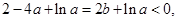

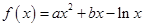 的单调区间判断必然通过导数方法来解决,伴随而来的是关于
的单调区间判断必然通过导数方法来解决,伴随而来的是关于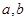 的分类讨论.比较
的分类讨论.比较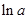 与
与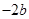 的大小时要根据已知条件和第一问的知识储备,构造新的函数利用单调性直接运算函数值得到结论.本题具备导数研究函数单调性的特征,必然按照程序化运行,即求导、关于参数分类讨论、确定单调区间等步骤进行.而第二问则是在第一问的基础上进一步挖掘解题素材,如隐含条件的发现、新函数的构造等,都为解决问题提供了有力支持.
的大小时要根据已知条件和第一问的知识储备,构造新的函数利用单调性直接运算函数值得到结论.本题具备导数研究函数单调性的特征,必然按照程序化运行,即求导、关于参数分类讨论、确定单调区间等步骤进行.而第二问则是在第一问的基础上进一步挖掘解题素材,如隐含条件的发现、新函数的构造等,都为解决问题提供了有力支持.

科目:高中数学 来源:不详 题型:解答题
 x2在(0,1 )上恒成立,求实数a的取值范围.
x2在(0,1 )上恒成立,求实数a的取值范围.查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
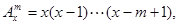 其中
其中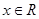 ,
,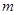 为正整数,且
为正整数,且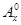 =1,这是排列数
=1,这是排列数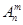 (
(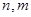 是正整数,
是正整数,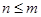 )的一种推广.
)的一种推广.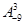 的值;
的值;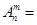
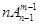 ,②
,②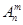
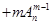
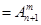 (其中m,n是正整数).是否都能推广到
(其中m,n是正整数).是否都能推广到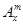 (
(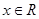 ,
,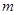 是正整数)的情形?若能推广,写出推广的形式并给予证明;若不能,则说明理由;
是正整数)的情形?若能推广,写出推广的形式并给予证明;若不能,则说明理由;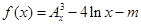 ,试讨论函数
,试讨论函数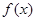 的零点个数.
的零点个数.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com