
分析 (1)根据幂函数的定义以及函数的奇偶性求出m的值,从而求出函数的解析式即可;
(2)法一:求出x+x-1,x-x-1,代入求值即可;法二:求出x的值,代入求值即可;法三:求出x+x-1,代数式变形平方即可.
解答 解:(1)由f(x)为幂函数知-2m2+m+2=1,得m=1或m=-$\frac{1}{2}$…(2分)
当m=1时,f(x)=x-1,是奇函数,不符合题意,舍去…(3分)
当m=-$\frac{1}{2}$时,f(x)=x2,是偶函数,符合题意,…(4分)
∴f(x)=x2…(5分)
(2)因为x2-x-2=(x+x-1)(x-x-1),
(x-x-1)2=(x+x-1)2-4,
又因为x+x-1=3,
∴(x+x-1)2=(x+x-1)2-4=5,
又因为x>1,所以x-x-1>0,
即x-x-1=$\sqrt{5}$,
所以x2-x-2=(x+x-1)(x-x-1)=3$\sqrt{5}$…(10分)
另解法2:由x+x-1=3,(x>1),得x2-3x+1=0,即x=$\frac{3+\sqrt{5}}{2}$,
所以x2-x-2=${(\frac{3+\sqrt{5}}{2})}^{2}$-${(\frac{3+\sqrt{5}}{2})}^{-2}$=$\frac{14+6\sqrt{5}}{4}$-$\frac{4}{14+6\sqrt{5}}$=$\frac{14+6\sqrt{5}}{4}$-$\frac{14-6\sqrt{5}}{4}$=3$\sqrt{5}$…(10分)
法3:由x+x-1=3,得(x+x-1)2=x2+x-2+2=9,
所以x2+x-2=7,
因为x2-x-2>0,
所以(x2-x-2)2=(x2+x-2)2-4=45,
即x2-x-2=3$\sqrt{5}$…(10分)
点评 本题考查了幂函数的定义,考查函数的奇偶性问题,考查代数式求值问题,是一道中档题.


 名题金卷系列答案
名题金卷系列答案科目:高中数学 来源: 题型:解答题
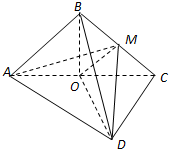 菱形ABCD的边长为3,AC与BD交于O,且∠BAD=60°.将菱形ABCD沿对角线AC折起得到三棱锥-ADC(如图),点M是棱C的中点,DM=$\frac{3\sqrt{2}}{2}$.
菱形ABCD的边长为3,AC与BD交于O,且∠BAD=60°.将菱形ABCD沿对角线AC折起得到三棱锥-ADC(如图),点M是棱C的中点,DM=$\frac{3\sqrt{2}}{2}$.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | c<b<a | B. | b<c<a | C. | a<b<c | D. | b<a<c |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 0 | B. | $\frac{7}{2}$ | C. | 4 | D. | $\frac{9}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com