
分析 (1)利用三角不等式证明:f(x)≥2;
(2)g(b)=$\frac{|2b+1|-|1-b|}{|b|}$≤$\frac{|2b+1-1+b|}{|b|}$=3,可得f(x)≥3,即|x-1|+|x+1|≥3,分类讨论,求x的取值范围.
解答 (1)证明:f(x)=|x-1|+|x+1|=|1-x|+|x+1|≥|1-x+x+1|=2;
(2)解:g(b)=$\frac{|2b+1|-|1-b|}{|b|}$≤$\frac{|2b+1-1+b|}{|b|}$=3,
∴f(x)≥3,即|x-1|+|x+1|≥3,
x≤-1时,-2x≥3,∴x≤-1.5,∴x≤-1.5;
-1<x≤1时,2≥3不成立;
x>1时,2x≥3,∴x≥1.5,∴x≥1.5.
综上所述x≤-1.5或x≥1.5.
点评 本题考查三角不等式,考查分类讨论的数学思想,考查学生的计算能力,属于中档题.


 出彩同步大试卷系列答案
出彩同步大试卷系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 2或-11 | B. | 2或-12 | C. | 1或-12 | D. | 1或-11 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
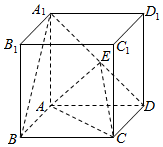 如图,在底面是菱形的四棱柱ABCD-A1B1C1D1中,∠ABC=60°,AA1=AC=2,A1B=A1D=2$\sqrt{2}$,点E在A1D上.
如图,在底面是菱形的四棱柱ABCD-A1B1C1D1中,∠ABC=60°,AA1=AC=2,A1B=A1D=2$\sqrt{2}$,点E在A1D上.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 3π | B. | 6 | C. | 12 | D. | 12π |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
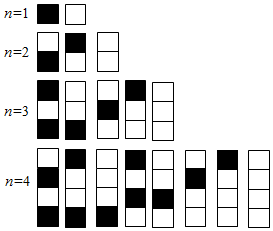 给n个自上而下相连的正方形着黑色或白色.当n≤4时,在所有不同的着色方案中,黑色正方形互不相邻的着色方案如图所示,由此推断,当n=6时,至少有两个黑色正方形相邻的着色方案共有( )种.
给n个自上而下相连的正方形着黑色或白色.当n≤4时,在所有不同的着色方案中,黑色正方形互不相邻的着色方案如图所示,由此推断,当n=6时,至少有两个黑色正方形相邻的着色方案共有( )种.| A. | 21 | B. | 32 | C. | 43 | D. | 54 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com