
【题目】已知双曲线![]() =1(a>0,b>0)的一条渐近线方程为2x+y=0,且顶点到渐近线的距离为
=1(a>0,b>0)的一条渐近线方程为2x+y=0,且顶点到渐近线的距离为![]() .
.
(1)求此双曲线的方程;
(2)设P为双曲线上一点,A,B两点在双曲线的渐近线上,且分别位于第一、二象限,若![]() ,求△AOB的面积.
,求△AOB的面积.
【答案】(1)![]() -x2=1;(2)2.
-x2=1;(2)2.
【解析】
(1)利用一条渐近线的离心率为2,和顶点到渐近线的距离列出两个等式结合![]() 求得
求得![]() 可得双曲线方程;
可得双曲线方程;
(2)设A(m,2m),B(-n,2n),其中m>0,n>0,![]() 说明P是AB的中点,由中点坐标公式得P点坐标,代入双曲线方程可求得
说明P是AB的中点,由中点坐标公式得P点坐标,代入双曲线方程可求得![]() ,设∠AOB=2θ,则有tan
,设∠AOB=2θ,则有tan![]() =2,由此可求得sin 2θ,再有|OA|=
=2,由此可求得sin 2θ,再有|OA|=![]() m,|OB|=
m,|OB|=![]() n,面积易求.
n,面积易求.
(1)依题意得 解得
解得![]()
故双曲线的方程为![]() -x2=1.
-x2=1.
(2)由(1)知双曲线的渐近线方程为y=±2x,设A(m,2m),B(-n,2n),其中m>0,n>0,由![]() 得点P的坐标为
得点P的坐标为![]() .
.
将点P的坐标代入![]() -x2=1,
-x2=1,
整理得mn=1.
设∠AOB=2θ,∵tan![]() =2,
=2,
则tan θ=![]() ,从而sin 2θ=
,从而sin 2θ=![]() .
.
又|OA|=![]() m,|OB|=
m,|OB|=![]() n,
n,
∴S△AOB=![]() |OA|·|OB|sin 2θ=2mn=2.
|OA|·|OB|sin 2θ=2mn=2.


科目:高中数学 来源: 题型:
【题目】某中学为了丰富学生的课外文体活动,分别开设了阅读、书法、绘画等文化活动;跑步、游泳、健身操等体育活动.该中学共有高一学生300名,要求每位学生必须选择参加其中一项活动,现对高一学生的性别、学习积极性及选择参加的文体活动情况进行统计,得到数据如下:

(1)在选择参加体育活动的学生中按性别分层抽取6名,再从这6名学生中抽取2人了解家庭情况,求2人中至少有1名女生的概率;
(2)是否有99.9%的把握认为学生的学习积极性与选择参加文化活动有关?请说明你的理由.
附:参考公式:![]() ,其中
,其中![]() .
.

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,已知抛物线![]() 和
和![]() ,过抛物线
,过抛物线![]() 上一点
上一点![]() 作两条直线与
作两条直线与![]() 分别相切于
分别相切于![]() 两点,分别交抛物线于
两点,分别交抛物线于![]() 两点.
两点.
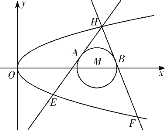
(1)当![]() 的角平分线垂直
的角平分线垂直![]() 轴时,求直线
轴时,求直线![]() 的斜率;
的斜率;
(2)若直线![]() 在
在![]() 轴上的截距为
轴上的截距为![]() ,求
,求![]() 的最小值.
的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在正方体![]() 中,点
中,点![]() 为棱
为棱![]() 上一动点(不包括顶点),平面
上一动点(不包括顶点),平面![]() 交
交![]() 于点
于点![]() ,则下列结论中错误的是( )
,则下列结论中错误的是( )
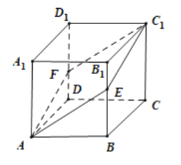
A.存在点![]() ,使得四边形
,使得四边形![]() 为菱形
为菱形
B.存在点![]() ,使得四边形
,使得四边形![]() 的面积最小
的面积最小
C.存在点![]() ,使得
,使得![]() 平面
平面![]()
D.存在点![]() ,使得平面
,使得平面![]() 平面
平面![]() (其中
(其中![]() 为
为![]() 的中点)
的中点)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知某班的50名学生进行不记名问卷调查,内容为本周使用手机的时间长,如表:
时间长(小时) |
|
|
|
|
|
女生人数 | 4 | 11 | 3 | 2 | 0 |
男生人数 | 3 | 17 | 6 | 3 | 1 |
(1)求这50名学生本周使用手机的平均时间长;
(2)时间长为![]() 的7名同学中,从中抽取两名,求其中恰有一个女生的概率;
的7名同学中,从中抽取两名,求其中恰有一个女生的概率;
(3)若时间长为![]() 被认定“不依赖手机”,
被认定“不依赖手机”,![]() 被认定“依赖手机”,根据以上数据完成
被认定“依赖手机”,根据以上数据完成![]() 列联表:
列联表:
不依赖手机 | 依赖手机 | 总计 | |
女生 | |||
男生 | |||
总计 |
能否在犯错概率不超过0.15的前提下,认为学生的性别与依赖手机有关系?
| 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
(参考公式:![]() ,
,![]() )
)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,某自来水公司要在公路两侧安装排水管,公路为东西方向,在路北侧沿直线![]() 排,在路南侧沿直线
排,在路南侧沿直线![]() 排,现要在矩形区域
排,现要在矩形区域![]() 内沿直线将
内沿直线将![]() 与
与![]() 接通.已知
接通.已知![]() ,
,![]() ,公路两侧排水管费用为每米1万元,穿过公路的
,公路两侧排水管费用为每米1万元,穿过公路的![]() 部分的排水管费用为每米2万元,设
部分的排水管费用为每米2万元,设![]() 与
与![]() 所成的小于
所成的小于![]() 的角为
的角为![]() .
.
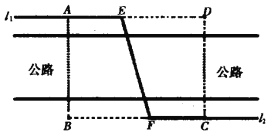
(Ⅰ)求矩形区域![]() 内的排水管费用
内的排水管费用![]() 关于
关于![]() 的函数关系;
的函数关系;
(Ⅱ)求排水管的最小费用及相应的角![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的左、右焦点分别为
的左、右焦点分别为![]() 、
、![]() ,焦距为
,焦距为![]() ,直线
,直线![]() :
:![]() 与椭圆相交于
与椭圆相交于![]() 、
、![]() 两点,
两点,![]() 关于直线
关于直线![]() 的对称点
的对称点![]() 在椭圆上.斜率为
在椭圆上.斜率为![]() 的直线
的直线![]() 与线段
与线段![]() 相交于点
相交于点![]() ,与椭圆相交于
,与椭圆相交于![]() 、
、![]() 两点.
两点.

(1)求椭圆的标准方程;
(2)求四边形![]() 面积的取值范围.
面积的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】十九大提出,加快水污染防治,建设美丽中国![]() 根据环保部门对某河流的每年污水排放量
根据环保部门对某河流的每年污水排放量![]() 单位:吨
单位:吨![]() 的历史统计数据,得到如下频率分布表:
的历史统计数据,得到如下频率分布表:
污水量 |
|
|
|
|
|
|
频率 |
|
|
|
|
|
|
将污水排放量落入各组的频率作为概率,并假设每年该河流的污水排放量相互独立.
(Ⅰ)求在未来3年里,至1年污水排放量![]() 的概率;
的概率;
(Ⅱ)该河流的污水排放对沿河的经济影响如下:当![]() 时,没有影响;当
时,没有影响;当![]() 时,经济损失为10万元;当
时,经济损失为10万元;当![]() 时,经济损失为60万元
时,经济损失为60万元![]() 为减少损失,现有三种应对方案:
为减少损失,现有三种应对方案:
方案一:防治350吨的污水排放,每年需要防治费![]() 万元;
万元;
方案二:防治310吨的污水排放,每年需要防治费2万元;
方案三:不采取措施.
试比较上述三种方案,哪种方案好,并请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com