
 甲、乙两名运动员在某项测试中的6次成绩如茎叶图所示,其中甲成绩的中位数为15,极差为12;乙成绩的众数为13,
甲、乙两名运动员在某项测试中的6次成绩如茎叶图所示,其中甲成绩的中位数为15,极差为12;乙成绩的众数为13,. |
| x1 |
. |
| x2 |
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
. |
| x1 |
. |
| x2 |
. |
| x1 |
| 9+14+15+15+16+21 |
| 6 |
. |
| x2 |
| 8+13+13+15+19+22 |
| 6 |
. |
| x1 |
. |
| x2 |


 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:
| x2 |
| a2 |
| y2 |
| b2 |
| x2 |
| a2 |
| y2 |
| b2 |
| a2+b2 |
| 2 |
| A、②③ | B、①②③ | C、①③ | D、② |
查看答案和解析>>
科目:高中数学 来源: 题型:
| A、a≥1 | B、a≤1 |
| C、a≥2 | D、a≤2 |
查看答案和解析>>
科目:高中数学 来源: 题型:
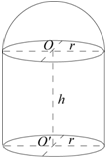 要设计一个金属容积为V(常数)的密闭容器,下部是圆柱形,上部为半球形(如图).当圆柱底面半径r与高h各为何值时,制造这个容器用料最省(表面积最小)?
要设计一个金属容积为V(常数)的密闭容器,下部是圆柱形,上部为半球形(如图).当圆柱底面半径r与高h各为何值时,制造这个容器用料最省(表面积最小)?查看答案和解析>>
科目:高中数学 来源: 题型:
| x2 |
| a2 |
| y2 |
| b2 |
| 1 |
| 2 |
| 3 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com