
分析 (1)求函数的导数,根据导数的几何意义即可得到结论.求a的值;
(2)将不等式恒成立转化为求函数的最值,求函数的导数,利用导数进行求解即可.
解答 解:(1)f′(x)=$\frac{(\frac{x+a}{x}+lnx)(x+1)-(x+a)lnx}{(x+1)^{2}}$,
∵y=f(x)在点(1,f(1))处的切线与直线2x+y+1=0垂直,
∴f′(1)=$\frac{1}{2}$,
∴$\frac{2(1+a)}{4}=\frac{1}{2}$,∴1+a=1,解得a=0.
(2)f(x)=$\frac{xlnx}{x+1}$,
若对于任意的x∈[1,+∞),f(x)≤m(x-1)恒成立,
即lnx≤m(x-$\frac{1}{x}$),
设g(x)=lnx-m(x-$\frac{1}{x}$),
即对于任意的x∈[1,+∞),g(x)≤0,
g′(x)=$\frac{1}{x}$-m(1+$\frac{1}{{x}^{2}}$)=$\frac{-m{x}^{2}+x-m}{{x}^{2}}$,
①若m≤0,g′(x)>0,则g(x)≥g(1)=0,这与题设g(x)≤0矛盾.
②若m>0,方程-mx2+x-m=0的判别式△=1-4m2,
当△≤0,即m≥$\frac{1}{2}$时,g′(x)≤0.
∴g(x)在(1,+∞)上单减,
∴g(x)≤g(1)=0,不等式成立.
当0<m<$\frac{1}{2}$时,方程-mx2+x-m=0,设两根为x1,x2,(x1<x2),
x1=$\frac{1-\sqrt{1-4{m}^{2}}}{2m}$∈(0,1),x2=$\frac{1+\sqrt{1-4{m}^{2}}}{2m}$∈(1,+∞),
当x∈(1,x1),g′(x)>0,g(x)单调递增,g(x)>g(1)=0,与题设矛盾.
综上所述,m≥$\frac{1}{2}$.
点评 本题主要考查导数的综合应用以及函数切线的求解,考查学生的运算能力,综合性较强,有一定的难度.


科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
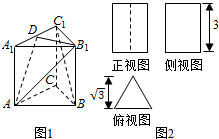 已知某几何体的直观图(图1)与它的三视图(图2),其中俯视图为正三角形,其它两个视图是矩形,已知D是棱A1C1的中点.
已知某几何体的直观图(图1)与它的三视图(图2),其中俯视图为正三角形,其它两个视图是矩形,已知D是棱A1C1的中点.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 甲校 | 乙校 | 丙校 | |
| 男生 | 97 | 90 | x |
| 女生 | 153 | y | z |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com