
分析 (I)利用递推关系、等比数列的通项公式即可得出.
(II)利用等比数列的前n项和公式、等差数列的通项公式即可得出.
解答 解:(Ⅰ)依题意,可得Sn=2-2an+1,①
当n≥2时,Sn-1=2-2an,②…(1 分)
①-②,得an=2an-2an+1,…(3 分)
故$\frac{{{a_{n+1}}}}{a_n}=\frac{1}{2}$(n≥2).…(4 分)
因为a1=1,${a_2}=1-\frac{a_1}{2}=\frac{1}{2}$,…(5 分)
所以{an}是首项为1,公比为$\frac{1}{2}$的等比数列,故${a_n}={(\frac{1}{2})^{n-1}}$.…(6 分)
(Ⅱ)解:由(Ⅰ)可得${S_n}=\frac{{1-{{(\frac{1}{2})}^n}}}{{1-\frac{1}{2}}}=2-\frac{1}{{{2^{n-1}}}}$.…(8 分)
由$\{{S_n}+λ(n+\frac{1}{2^n})\}$为等差数列,
则${S_1}+λ(1+\frac{1}{2})$,${S_2}+λ(2+\frac{1}{4})$,${S_3}+λ(3+\frac{1}{8})$成等差数列.…(10分)
即$2({S_2}+\frac{9λ}{4})={S_1}+\frac{3λ}{2}+{S_3}+\frac{25λ}{8}$,
故$2(\frac{3}{2}+\frac{9λ}{4})=1+\frac{3λ}{2}+\frac{7}{4}+\frac{25λ}{8}$,…(12分)
解得λ=2.…(13分)
点评 本题考查了等差数列与等比数列的通项公式及其前n项和公式、递推关系,考查了推理能力与计算能力,属于中档题.


 星级口算天天练系列答案
星级口算天天练系列答案科目:高中数学 来源: 题型:选择题
| A. | $({1,\sqrt{2}})$ | B. | $({1,\sqrt{2}}]$ | C. | $({\sqrt{2},+∞})$ | D. | $[{\sqrt{2},+∞})$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\sqrt{3}$ | B. | $\sqrt{5}$ | C. | 3 | D. | $\frac{\sqrt{5}}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
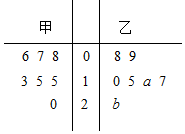 甲、乙两家快餐店对某日7个时段光顺的客人人数进行统计并绘制茎叶图如图所示(下面简称甲数据、乙数据),且乙数据的众数为17,甲数据的平均数比乙数据平均数少2.
甲、乙两家快餐店对某日7个时段光顺的客人人数进行统计并绘制茎叶图如图所示(下面简称甲数据、乙数据),且乙数据的众数为17,甲数据的平均数比乙数据平均数少2.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 充分而不必要条件 | B. | 必要而不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 3 | B. | 4 | C. | $\frac{1}{4}$ | D. | $\frac{1}{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -$\frac{3}{2}$ | B. | $\frac{3}{2}$ | C. | -6 | D. | 6 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 3 | B. | $\sqrt{3}$ | C. | $\frac{\sqrt{3}}{3}$ | D. | $\frac{1}{3}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com