科目：高中数学 来源：2017届湖北省协作校高三联考一数学（理）试卷（解析版） 题型：解答题
已知函数
的定义域为
，
，函数
的值域为
．
（1）当
时，求
；
（2）是否存在实数
，使得
？若存在，求出
的值；若不存在，请说明理由．
查看答案和解析>>
科目：高中数学 来源：2016-2017学年河南八市高二文上月考一数学试卷（解析版） 题型：解答题
设
是等差数列，
是各项都为正数的等比数列，且
，
，
.
（1）求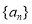
，
的通项公式；
（2）求数列
的前
项和
.
查看答案和解析>>
科目：高中数学 来源：2016-2017学年河南八市高二文上月考一数学试卷（解析版） 题型：填空题
某公司租赁甲、乙两种设备生产
两类产品，甲种设备每天能生产
类产品5件和
类产品10件，乙种设备每天能生产
类产品6件和
类产品20件.已知设备甲每天的租赁费为200元，设备乙每天的租赁费用为300元，现该公司至少要生产
类产品50件，
类产品140件，所需租赁费最少为__________元.
查看答案和解析>>
科目：高中数学 来源：2016-2017学年河南八市高二文上月考一数学试卷（解析版） 题型：选择题
若变量
满足约束条件
，则目标函数
的最小值为（ ）
A．-5 B．-4
C.-2 D．3
查看答案和解析>>
科目：高中数学 来源：2016-2017学年重庆市高一上学期第一次月考数学试卷（解析版） 题型：填空题
我们知道平方运算和开方运算是互逆运算，如：
，那么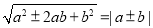
，那么如何将双重二次根式
化简呢？如能找到两个数
，使得
即
，且使
即
，那么
，双重二次根式得以化简；例如化简：
； 
且
，
由此对于任意一个二次根式只要可以将其化成的形式，且能找到
使得
，且
，那么这个双重二次根式一定可以化简为一个二次根式．请同学们通过阅读上述材料，完成下列问题：
（1）填空：
_________________；
__________________；
（2）化简：①
②
（每题2分）
（3）计算：
查看答案和解析>>
科目：高中数学 来源： 题型：选择题
| A． | （-∞，-5）∪（1，+∞） | B． | （1，19） | C． | [1，19） | D． | （19，+∞） |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
在平面区域
上，点
在曲线
上，那么
的最小值为（ ）
B．
C. 
D．
的定义域是_________.
的解组成的集合是 （ ）
