练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    当x>0时，求证：ex>x+1.

    分析：本题考查利用导数证明不等式的问题.解题的关键是由导数确定单调区间，由函数在某一区间上的单调性构造不等式求解.

    证明不妨设f(x)=ex-x-1,

    则f′(x)=(ex)′-(x)′=ex-1.

    ∵x>0,∴ex>1,ex-1>0.

    ∴f′(x)>0,即f(x)在（0，+∞)上是增函数.

    ∴f(x)>f(0),即ex-x-1>e0-1=0.

    ∴ex>x+1.

    点评：利用导数可证明不等式:若函数y=f(x)在x∈(a,b)上是单调增函数,任取a<x<b,则f(x)>f(a),f(x)<f(b);若函数y=f(x)在x∈(a,b)上是单调减函数,任取a<x<b,则f(x)<f(a),f(x)>f(b).

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    已知函数f（x）=ax2+ln（x+1）．
    （Ⅰ）当a=-
    1
    4
    时，求函数f（x）的单调区间；
    （Ⅱ）当x∈[0，+∞）时，不等式f（x）≤x恒成立，求实数a的取值范围．
    （Ⅲ）求证：(1+
    1
    1×2
    )(1+
    1
    2×3
    )•…•[1+
    1
    n(n+1)
    ]＜e    （n∈N*，e是自然对数的底数）．
    提示：[ln(x+1)]′=
    1
    x+1
    ．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    已知函数f（x）=ax2+ln（x+1）．
    （1）当a=-
    1
    4
    时，求函数f（x）的单调区间；
    （2）当x∈[0，+∞）时，不等式f（x）≤x恒成立，求实数a的取值范围．
    （3）利用ln（x+1）≤x，求证：ln{(1+
    2
    2×3
    )(1+
    4
    3×5
    )(1+
    8
    5×9
    )•…•[1+
    2n
    (2n-1+1)(2n+1)
    ]}＜1    （其中n∈N*，e是自然对数的底数）．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    已知函数，f（x）=x2，g（x）=2eln（x＞0）（e为自然对数的底数），它们的导数分别为f′（x）、g′（x）．
    （1）当x＞0时，求证：f′（x）+g′（x）≥4
    		e
    ；
    （2）求F（x）=f（x）-g（x）（x＞0）的单调区间及最小值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：044

    (2007成都模拟)已知函数f(x)=xln x．

    (1)求函数f(x)的单调区间和最小值；

    (2)当b＞0时，求证:(其中e=2.71828…是自然对数的底数)；

    (3)若a＞0，b＞0，证明：f(a)＋(a＋b)ln2≥f(a＋b)－f(b).

    查看答案和解析>>

    科目：高中数学 来源： 题型：

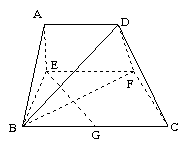
    （08年周至二中二模理）已知梯形ABCD中，AD∥BC，∠ABC =∠BAD =，AB=BC=2AD=4，E、F分别是AB、CD上的点，EF∥BC，AE = x，G是BC的中点。沿EF将梯形ABCD翻折，使平面AEFD⊥平面EBCF (如图) .

    (1) 当x=2时，求证：BD⊥EG ；

    (2) 若以F、B、C、D为顶点的三棱锥的体积记为f(x)，求f(x)的最大值；

    (3) 当 f(x)取得最大值时，求二面角D-BF-C的余弦值.

                                     

    查看答案和解析>>

    同步练习册答案