
【题目】已知函数![]() ,(其中
,(其中![]() ,
,![]() 为自然对数的底数).
为自然对数的底数).
(1)讨论函数![]() 的单调性;
的单调性;
(2)若![]() 分别是
分别是![]() 的极大值点和极小值点,且
的极大值点和极小值点,且![]() ,求证:
,求证:![]() .
.
【答案】(1)见解析;(2)证明见解析
【解析】
(1)讨论![]() ,
,![]() 和
和![]() 三种情况,分别计算得到答案.
三种情况,分别计算得到答案.
(2)根据题意知![]() 等价于
等价于![]() ,设
,设
![]() ,计算得到
,计算得到![]() 使
使![]() ,计算得到
,计算得到
![]() 得到证明.
得到证明.
(1)当![]() 时,
时,![]() ,
,
![]() 的单调递增区间是
的单调递增区间是![]() ,单调递减区间是
,单调递减区间是![]() ;
;
![]() 时,
时,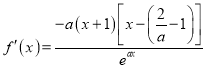 ,
,
①![]() 时,由
时,由![]() 解得
解得![]() 或
或![]() ;由
;由![]() 解得
解得![]() ,
,![]() 的单调递增区间是
的单调递增区间是![]() 和
和![]() ,单调递减区间是
,单调递减区间是![]()
②![]() 时,由
时,由![]() 解得
解得![]() ;由
;由![]() 解得
解得![]() 或
或![]() ,
,![]() 的单调递增区间是
的单调递增区间是![]() ,单调递减区间是
,单调递减区间是![]() 和
和![]() ;
;
综上所述:
![]() 时,单调递增区间是
时,单调递增区间是![]() ,单调递减区间是
,单调递减区间是![]() ;
;
![]() 时,单调递增区间是
时,单调递增区间是![]() 和
和![]() ,单调递减区间是
,单调递减区间是![]() ;
;
![]() 时,单调递增区间是
时,单调递增区间是![]() ,单调递减区间是
,单调递减区间是![]() 和
和![]() ;
;
(2)由已知和(1)得,当![]() 时满足题意,此时
时满足题意,此时![]() ,
, ![]() ,
,
令![]() ,则
,则![]() .
.
令![]() 则
则![]() 恒成立,
恒成立,
![]() 在
在![]() 上单调递增,
上单调递增,
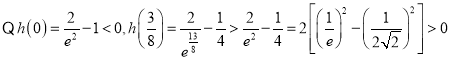
![]() 使
使![]() ,即
,即![]()
从而当![]() 时,
时, ![]() 单调递减,当
单调递减,当![]() 时,
时, ![]() 单调递增,
单调递增,
![]()
![]() 在
在![]() 上单调递减
上单调递减
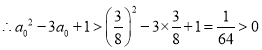 ,
,![]() ,
,
即![]() ,
,![]()


科目:高中数学 来源: 题型:
【题目】如图1为某省2018年1~4月快递业务量统计图,图2是该省2018年1~4月快递业务收入统计图,下列对统计图理解错误的是( )


A. 2018年1~4月的业务量,3月最高,2月最低,差值接近2000万件
B. 2018年1~4月的业务量同比增长率均超过50%,在3月底最高
C. 从两图来看,2018年1~4月中的同一个月的快递业务量与收入的同比增长率并不完全一致
D. 从1~4月来看,该省在2018年快递业务收入同比增长率逐月增长
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在等比数列{an}中,an>0 (n∈N ),公比q∈(0,1),且a1a5+2a3a5+a2a8=25,又a3与a5的等比中项为2.
(1) 求数列{an}的通项公式;
(2) 设![]() ,数列{bn}的前n项和为Sn,当
,数列{bn}的前n项和为Sn,当![]() 最大时,求n的值.
最大时,求n的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知各项均不相等的等差数列{an}的前n项和为Sn,若S3=15,且a3+1为a1+1和a7+1的等比中项.
(1)求数列{an}的通项公式与前n项和Sn;
(2)设Tn为数列{![]() }的前n项和,问是否存在常数m,使Tn=m[
}的前n项和,问是否存在常数m,使Tn=m[![]() +
+![]() ],若存在,求m的值;若不存在,说明理由.
],若存在,求m的值;若不存在,说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列说法正确的是( )
A.两条相交直线在同一平面内的射影必为相交直线
B.不共线三点到平面![]() 的距离相等,则这三点确定的平面不一定与平面
的距离相等,则这三点确定的平面不一定与平面![]() 平行
平行
C.对确定的两异面直线,过空间任一点有且只有一个平面与两异面直线都平行
D.两个相交平面的交线是一条线段
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,椭圆C:![]() 的右准线方程为x=2,且两焦点与短轴的一个顶点构成等腰直角三角形.
的右准线方程为x=2,且两焦点与短轴的一个顶点构成等腰直角三角形.
(1)求椭圆C的方程;
(2)假设直线l:![]() 与椭圆C交于A,B两点.①若A为椭圆的上顶点,M为线段AB中点,连接OM并延长交椭圆C于N,并且
与椭圆C交于A,B两点.①若A为椭圆的上顶点,M为线段AB中点,连接OM并延长交椭圆C于N,并且![]() ,求OB的长;②若原点O到直线l的距离为1,并且
,求OB的长;②若原点O到直线l的距离为1,并且![]() ,当
,当![]() 时,求△OAB的面积S的范围.
时,求△OAB的面积S的范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某市有![]() ,
,![]() 两家乒乓球俱乐部,两家的设备和服务都很好,但收费标准不同,
两家乒乓球俱乐部,两家的设备和服务都很好,但收费标准不同,![]() 俱乐部每张球台每小时5元,
俱乐部每张球台每小时5元,![]() 俱乐部按月收费,一个月中
俱乐部按月收费,一个月中![]() 以内(含
以内(含![]() )每张球台90元,超过
)每张球台90元,超过![]() 的部分每张球台每小时加收2元.某学校准备下个月从这两家中的一家租一张球台开展活动,其活动时间不少于
的部分每张球台每小时加收2元.某学校准备下个月从这两家中的一家租一张球台开展活动,其活动时间不少于![]() ,也不超过
,也不超过![]() .
.
(1)设在![]() 俱乐部租一-张球台开展活动
俱乐部租一-张球台开展活动![]() 的收费为
的收费为![]() 元
元![]() ,在
,在![]() 俱乐部租一张球台开展活动
俱乐部租一张球台开展活动![]() 的收费为
的收费为![]() 元
元![]() ,试求
,试求![]() 和
和![]() 的解析式;
的解析式;
(2)问选择哪家俱乐部比较合算?为什么?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】曾玉、刘云、李梦、张熙四人被北京大学、清华大学、武汉大学和复旦大学录取,他们分别被哪个学校录取,同学们做了如下的猜想
甲同学猜:曾玉被武汉大学录取,李梦被复旦大学录取
同学乙猜:刘云被清华大学录取,张熙被北京大学录取
同学丙猜:曾玉被复旦大学录取,李梦被清华大学录取
同学丁猜:刘云被清华大学录取,张熙被武汉大学录取
结果,恰好有三位同学的猜想各对了一半,还有一位同学的猜想都不对
那么曾玉、刘云、李梦、张熙四人被录取的大小可能是( )
A.北京大学、清华大学、复旦大学、武汉大学
B.武汉大学、清华大学、复旦大学、北京大学
C.清华大学、北京大学、武汉大学 、复旦大学
D.武汉大学、复旦大学、清华大学、北京大学
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com