
分析 (1)设点N(x,y),由已知得|MN|=2|OM|,由此能求出点N的轨迹曲线C的方程,由曲线C是以(-1,0)为圆心,以r=2为半径的圆,能求出过点P且与曲线C相切的直线的方程.
(2)当直线l的斜率不存在时,直线l的方程为x=0,此时△PAB面积S△PAB=2$\sqrt{3}$.当直线l的斜率存在时,设直线l的方程为y=mx,m≠0,联立$\left\{\begin{array}{l}{y=mx}\\{(x+1)^{2}+{y}^{2}=4}\end{array}\right.$,得(1+m2)x2+2x-3=0,由此利用根的判别式、韦达定理、弦长公式能求出△PAB面积的取值范围.
解答 解:(1)设点N(x,y),∵点N到原点O与到点M(3,0)的距离之比为$\frac{1}{2}$,
∴$\frac{|ON|}{|MN|}$=$\frac{1}{2}$,∴|MN|=2|OM|,
∴$\sqrt{(x-3)^{2}+{y}^{2}}$=2$\sqrt{{x}^{2}+{y}^{2}}$,
两边平方整理,得点N的轨迹曲线C的方程为:x2+y2+2x-3=0,
即(x+1)2+y2=4,
∴曲线C是以(-1,0)为圆心,以r=2为半径的圆,
当过点P(2,0)且与曲线C相切的直线的斜率不存在时,直线方程为x=2,
圆心C(-1,0)到直线x=2的距离为3≠r=2,不成立.
当直线的斜率存在时,设直线方程为y=k(x-2),
∵圆心C(-1,0)到切线y=k(x-2)的距离等于半径r=2,
∴$\frac{|3k|}{\sqrt{{k}^{2}+1}}$=2,解得k=±$\frac{2\sqrt{5}}{5}$,
∴过点P且与曲线C相切的直线的方程为y=$±\frac{2\sqrt{5}}{5}$(x-2).
(2)当直线l的斜率不存在时,直线l的方程为x=0,
联立$\left\{\begin{array}{l}{x=0}\\{(x+1)^{2}+{y}^{2}=4}\end{array}\right.$,得A(0,$\sqrt{3}$),B(0,-$\sqrt{3}$),
|AB|=2$\sqrt{3}$,点P(2,0)到直线AB的距离d=2,
此时△PAB面积S△PAB=$\frac{1}{2}×|AB|×d$=$\frac{1}{2}×2\sqrt{3}×2$=2$\sqrt{3}$.
当直线l的斜率存在时,设直线l的方程为y=mx,m≠0,
联立$\left\{\begin{array}{l}{y=mx}\\{(x+1)^{2}+{y}^{2}=4}\end{array}\right.$,得(1+m2)x2+2x-3=0,
△=4+12(1+m2)>0,
设A(x1,y1),B(x2,y2),则${x}_{1}+{x}_{2}=-\frac{2}{1+{m}^{2}}$,x1x2=-$\frac{3}{1+{m}^{2}}$,
|AB|=$\sqrt{1+{m}^{2}}$•$\sqrt{(-\frac{2}{1+{m}^{2}})^{2}-4×(-\frac{3}{1+{m}^{2}})}$=2$\sqrt{\frac{4+3{m}^{2}}{1+{m}^{2}}}$,
点P(2,0)到直线y=mx的距离d=$\frac{|2m|}{\sqrt{1+{m}^{2}}}$,
∴△PAB面积S△PAB=$\frac{1}{2}|AB|•d$=$\frac{1}{2}×2\sqrt{\frac{4+3{m}^{2}}{1+{m}^{2}}}×\frac{|2m|}{\sqrt{1+{m}^{2}}}$=$\frac{2|m|\sqrt{4+3{m}^{2}}}{1+{m}^{2}}$=2$\sqrt{\frac{4+3{m}^{2}}{{m}^{2}+\frac{1}{{m}^{2}}+2}}$,
∴由${m}^{2}+\frac{1}{{m}^{2}}+2$≥4,(当且仅当${m}^{2}=\frac{1}{{m}^{2}}$,即m2=1时取等号),
得当m2=1时,△PAB面积最小值(S△PAB)min=2$\sqrt{\frac{4+3}{4}}$=$\sqrt{7}$.
又$\underset{lim}{n→∞}(2\sqrt{\frac{4+3{m}^{2}}{{m}^{2}+\frac{1}{{m}^{2}}+2}})$=2$\sqrt{3}$,
∴△PAB面积的取值范围是[$\sqrt{7}$,2$\sqrt{3}$].
点评 本题考查过已知点与曲线相切的直线方程的求法,考查三角形的面积的取值范围的求法,是中档题,解题时要认真审题,注意根的判别式、韦达定理、弦长公式的合理运用.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 采用系统抽样法从某班按学号抽取5名同学参加活动,学号为4,15,26,37,48的同学均被选出,则该班学生人数可能为55 | |
| B. | “x<0”是“ln(x+1)<0”的必要不充分条件 | |
| C. | “?x≥2,x2-3x+2≥0”的否定是?x<2,x2-3x+2<0 | |
| D. | x<3是-1<x<3的必要不充分条件 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
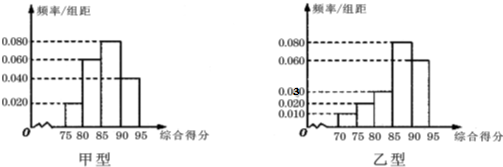
| 综合得分K的范围 | 节排器等级 |
| K≥85 | 一级品 |
| 75≤k<85 | 二级品 |
| 70≤k<75 | 三级品 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com