
【题目】给出下列命题:
(1)存在实数![]() 使
使![]() ;
;
(2)直线![]() 是函数
是函数![]() 图象的一条对称轴;
图象的一条对称轴;
(3)![]() (
(![]() )的值域是
)的值域是![]() ;
;
(4)若![]() ,
,![]() 都是第一象限角,且
都是第一象限角,且![]() ,则
,则![]() .
.
其中正确命题的序号为( )
A.(1)(2)B.(2)(3)C.(3)(4)D.(1)(4)
【答案】B
【解析】
(1)利用辅助角公式将![]() 可判断(1);
可判断(1);
(2)根据函数y=sinx图象的对称轴方程可判断(2);
(3)根据余弦函数的性质可求出y=cos(cosx)(x∈R)的最大值与最小值,从而可判断(3)的正误;
(4)用特值法令α,β都是第一象限角,且α>β,可判断(4).
解:(1)∵![]() ,∴(1)错误;
,∴(1)错误;
(2)∵y=sinx图象的对称轴方程为![]() ,k=﹣1,
,k=﹣1,![]() ,∴(2)正确;
,∴(2)正确;
(3)根据余弦函数的性质可得cosx![]() , y=cos(cosx)的最大值为ymax=cos0=1,ymin=cos(cos1),其值域是[cos1,1],(3)正确;
, y=cos(cosx)的最大值为ymax=cos0=1,ymin=cos(cos1),其值域是[cos1,1],(3)正确;
(4)不妨令![]() ,满足α,β都是第一象限角,且α>β,但tanα<tanβ,(4)错误;
,满足α,β都是第一象限角,且α>β,但tanα<tanβ,(4)错误;
故选:B.


 名校练考卷期末冲刺卷系列答案
名校练考卷期末冲刺卷系列答案科目:高中数学 来源: 题型:
【题目】已知某产品的销售额![]() 与广告费用
与广告费用![]() 之间的关系如下表:
之间的关系如下表:
| 0 | 1 | 2 | 3 | 4 |
| 10 | 15 |
| 30 | 35 |
若根据表中的数据用最小二乘法求得![]() 对
对![]() 的回归直线方程为
的回归直线方程为![]() ,则下列说法中错误的是( )
,则下列说法中错误的是( )
A.产品的销售额与广告费用成正相关
B.该回归直线过点![]()
C.当广告费用为10万元时,销售额一定为74万元
D.![]() 的值是20
的值是20
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】将6名党员干部分配到4个贫困村驻村扶贫,每个贫困村至少分配1名党员干部,则不同的分配方案共有( )
A.2640种B.4800种C.1560种D.7200种
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在直角坐标系![]() 中,曲线C的参数方程为
中,曲线C的参数方程为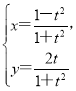 (t为参数),以坐标原点O为极点,x轴的正半轴为极轴建立极坐标系,直线
(t为参数),以坐标原点O为极点,x轴的正半轴为极轴建立极坐标系,直线![]() 的极坐标方程为
的极坐标方程为![]() .
.
(1)求C的普通方程和![]() 的直角坐标方程;
的直角坐标方程;
(2)求C上的点到![]() 距离的最大值.
距离的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
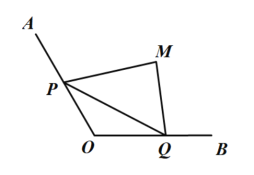
【题目】某沿海特区为了缓解建设用地不足的矛盾,决定进行围海造陆以增加陆地面积.如图,两海岸线![]() ,
,![]() 所成角为
所成角为![]() ,现欲在海岸线
,现欲在海岸线![]() ,
,![]() 上分别取点
上分别取点![]() ,
,![]() 修建海堤,以便围成三角形陆地
修建海堤,以便围成三角形陆地![]() ,已知海堤
,已知海堤![]() 长为6千米.
长为6千米.
(1)如何选择![]() ,
,![]() 的位置,使得
的位置,使得![]() 的面积最大;
的面积最大;
(2)若需要进一步扩大围海造陆工程,在海堤![]() 的另一侧选取点
的另一侧选取点![]() ,修建海堤
,修建海堤![]() ,
,![]() 围成四边形陆地.当海堤
围成四边形陆地.当海堤![]() 与
与![]() 的长度之和为10千米时,求四边形
的长度之和为10千米时,求四边形![]() 面积的最大值.
面积的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知 m、n 是两条不同的直线,α、β、γ是三个不同的平面,下列命题中正确的是( )
A.若α⊥β , β⊥γ ,则α∥γ
B.若 ![]() ,
, ![]() , m∥n ,则α∥β
, m∥n ,则α∥β
C.若 m、n 是异面直线, ![]() , m∥β ,
, m∥β , ![]() , n∥α ,则α∥β
, n∥α ,则α∥β
D.平面α内有不共线的三点到平面 β的距离相等,则α∥β
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】《中国诗词大会》是由CCTV-10自主研发的一档大型文化益智节目,以“赏中华诗词,寻文化基因品生活之美”为宗旨,带动全民重温经典、从古人的智慧和情怀中汲取营养、涵养心灵,节目广受好评还因为其颇具新意的比赛规则:每场比赛,106位挑战者全部参赛,分为单人追逐赛和擂主争霸赛两部分单人追逐赛的最终优胜者作为攻擂者与守擂擂主进行比拼,竞争该场比赛的擂主,擂主争霸赛以抢答的形式展开,共九道题,抢到并回答正确者得一分,答错则对方得一分,先得五分者获胜,成为本场擂主,比赛结束已知某场擂主争霸赛中,攻擂者与守擂擂主都参与每一次抢题且两人抢到每道题的概率都是![]() ,攻擂者与守擂擂主正确回答每道题的概率分别为
,攻擂者与守擂擂主正确回答每道题的概率分别为![]() ,
,![]() ,且两人各道题是否回答正确均相互独立.
,且两人各道题是否回答正确均相互独立.
(1)比赛开始,求攻擂者率先得一分的概率;
(2)比赛进行中,攻擂者暂时以![]() 领先,设两人共继续抢答了
领先,设两人共继续抢答了![]() 道题比赛结束,求随机变量
道题比赛结束,求随机变量![]() 的分布列和数学期望.
的分布列和数学期望.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com