
若函数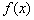 满足:集合
满足:集合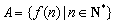 中至少存在三个不同的数构成等比数列,则称函数
中至少存在三个不同的数构成等比数列,则称函数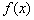 是等比源函数.
是等比源函数.
(Ⅰ)判断下列函数:①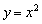 ;②
;②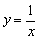 ;③
;③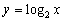 中,哪些是等比源函数?(不需证明)
中,哪些是等比源函数?(不需证明)
(Ⅱ)判断函数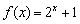 是否为等比源函数,并证明你的结论;
是否为等比源函数,并证明你的结论;
(Ⅲ)证明: ,函数
,函数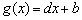 都是等比源函数.
都是等比源函数.
 名题金卷系列答案
名题金卷系列答案科目:高中数学 来源: 题型:
如果小明在某一周的第一天和第七天分别吃了3个水果,且从这周的第二天开始,每天所吃水果的个数与前一天相比,仅存在三种可能:或“多一个”或“持平”或“少一个”,那么,小明在这一周中每天所吃水果个数的不同选择方案共有
A.50种 B.51种 C.140种 D.141种
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com