
设函数 ,
, ,其中
,其中 为实数,若
为实数,若 在
在 上是单调减函数,且
上是单调减函数,且 在
在 上有最小值,求
上有最小值,求 的取值范围.
的取值范围.
a∈(e,+∞)
【解析】
试题分析:分别利用导数求出 单调区间与
单调区间与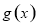 在
在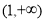 上的最小值,与给定的
上的最小值,与给定的 在
在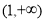 上是单调减函数,且
上是单调减函数,且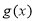 在
在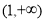 上有最小值相结合,得出关于
上有最小值相结合,得出关于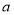 的关系式,可得
的关系式,可得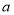 的取值范围.
的取值范围.
【解析】
令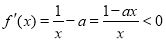 ,
,
考虑到f(x)的定义域为(0,+∞),故a>0,进而解得x>a-1,即f(x)在(a-1,+∞)上是单调减函数,
同理,f(x)在(0,a-1)上是单调增函数.
由于f(x)在(1,+∞)上是单调减函数,故(1,+∞)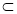 (a-1,+∞),从而a-1≤1,即a≥1,
(a-1,+∞),从而a-1≤1,即a≥1,
令g'(x)=ex-a=0,得 .
.
当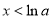 时,
时, 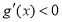 ;当x>
;当x>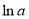 时,
时, 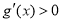 .
.
又g(x)在(1,+∞)上有最小值,所以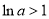 ,
,
即a>e.综上,有a∈(e,+∞).
考点:利用导数求函数的单调区间与最值.


科目:高中数学 来源:2015届安徽省铜陵市高二下学期月考数学试卷(解析版) 题型:选择题
无论m为任何实数,直线l:y=x+m与双曲线C: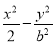 =1(b>0)恒有公共点,则双曲线C的离心率e的取值范围是( )
=1(b>0)恒有公共点,则双曲线C的离心率e的取值范围是( )
A.(1,+∞) B.(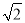 ,+∞) C.(
,+∞) C.(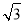 ,+∞) D.(2,+∞)
,+∞) D.(2,+∞)
查看答案和解析>>
科目:高中数学 来源:2015届安徽师大附中高二下学期期中考查文科数学试卷(解析版) 题型:选择题
若抛物线
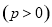 的焦点与双曲线
的焦点与双曲线 的右焦点重合,则
的右焦点重合,则 的值为( )
的值为( )
A.8 B.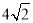 C.4 D.2
C.4 D.2
查看答案和解析>>
科目:高中数学 来源:2015届宁夏高二下学期期中考试理科数学试卷(解析版) 题型:选择题
一物体在力 (单位:N)的作用下沿与力
(单位:N)的作用下沿与力 相同的方向,从x=0处运动到
相同的方向,从x=0处运动到 (单位:
(单位:  )处,则力
)处,则力 做的功为( )
做的功为( )
A.44 B.46 C.48 D.50
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com