
分析 (1)利用辅助角公式将函数进行化简,利用三角函数的周期公式进行计算即可.
(2)法一、把函数解析式变形:y=|sinx|+|cosx|=$\sqrt{1+|sin2x|}$,由此求得函数周期;法二、利用周期定义求解.
解答 解:(1)y=cos2x+sin2x=$\sqrt{2}$sin(2x+$\frac{π}{4}$),
则三角函数的周期T=$\frac{2π}{2}$=π.
(2)法一、
∵y=|sinx|+|cosx|>0,
∴y2=sin2x+cos2x+2|sinx||cosx|
=1+|sin2x|,
∴y=$\sqrt{1+|sin2x|}$,即y=|sinx|+|cosx|=$\sqrt{1+|sin2x|}$,
∵函数y=sin2x的周期为π,
∴y=|sin2x|的周期为$\frac{π}{2}$,
故y=|sinx|+|cosx|的周期为$\frac{π}{2}$;
法二、
∵|sin(x+$\frac{π}{2}$)|+|cos(x+$\frac{π}{2}$)|=|cosx|+|-sinx|=|sinx|+|cosx|,
∴函数y=|sinx|+|cosx|的周期为$\frac{π}{2}$.
点评 本题主要考查三角函数的周期的计算,利用辅助角公式以及两角和差的正弦公式是解决本题的关键,体现了数学转化思想方法,是中档题.


科目:高中数学 来源: 题型:解答题
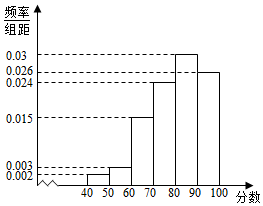 作为市政府为民办实事之一的公共自行车建设工作已经基本完成了,相关部门准备对该项目进行验收,验收的硬性指标是:市民对该项目的满意指数不低于0.8,否则该项目需进行整改,该部门为了了解市民对该项目的满意程度,在公共自行车自助点随机访问了前来使用的100名市民,并根据这100名市民对该项目满意程度的评分(满分100分),绘制了如图频率分布直方图:
作为市政府为民办实事之一的公共自行车建设工作已经基本完成了,相关部门准备对该项目进行验收,验收的硬性指标是:市民对该项目的满意指数不低于0.8,否则该项目需进行整改,该部门为了了解市民对该项目的满意程度,在公共自行车自助点随机访问了前来使用的100名市民,并根据这100名市民对该项目满意程度的评分(满分100分),绘制了如图频率分布直方图:查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 5 | B. | 5-2$\sqrt{2}$ | C. | 5-2$\sqrt{3}$ | D. | 5+2$\sqrt{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | y=2x-$\frac{1}{{2}^{x}}$ | B. | y=ln$\sqrt{1-{x}^{2}}$ | C. | y=x2-2x | D. | y=x2+2x |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com