
����Ŀ��ij�����̴����ˮ����ֳ������һ��С��Ϻ���������ȡ40ֻ����ͳ�ƣ�����������ͳ�ƽ����ͼ�� 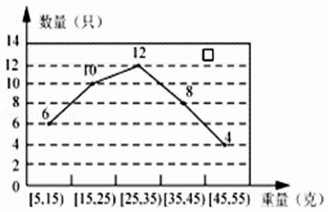
��1�����¼�AΪ����������С��Ϻ����ȡһֻ������������35g��С��Ϻ������P��A���Ĺ���ֵ��
��2������������С��Ϻ100ǧ�ˣ��Թ�������С��Ϻ��������
��3��Ϊ��Ӧ�г������˽�����С��Ϻ�ĿڸУ��þ����̽���40ֻС��Ϻ�ֳ������ȼ������±���
�ȼ� | һ��Ʒ | ����Ʒ | ����Ʒ |
������g�� | [5��25�� | [25��45�� | [45��55] |
���ֲ������ȡ10ֻ���������ȡ3ֻƷ������XΪ�鵽����Ʒ����������鵽����Ʒ��������
���𰸡�
��1���⣺����40ֻС��Ϻ������������35g��С��Ϻ��6+10+12=28��ֻ��
���� ![]() ��
��
��2���⣺��ͳ��ͼ�п��Թ���ÿֻС��Ϻ������ ![]()
= ![]() ���ˣ�
���ˣ�
���Թ���100ǧ�ˣ�С��Ϻ������Լ��100000��28.5��3509��ֻ��
��3���⣺������֪��ȡһ��Ʒ������Ʒ������Ʒ�ֱ�Ϊ4ֻ��5ֻ��1ֻ��X=0��1��2��3
��ɵ� ![]() ��
�� ![]() ��
��
![]() ��
�� ![]()
���� ![]() ��
��
����������1������40ֻС��Ϻ������������35g��С��Ϻ��6+10+12��ֻ�������ùŵ���ʼ��㹫ʽ���ɵó�����2�������ƽ�������ɵô�ͳ��ͼ�п��Թ���ÿֻС��Ϻ����������3��������֪��ȡһ��Ʒ������Ʒ������Ʒ�ֱ�Ϊ4ֻ��5ֻ��1ֻ��X=0��1��2��3�����ó����ηֲ��еĸ���
�ļ��㹫ʽ���ɵó���
�����㾫����������Ĺؼ�����������ɢ�������������ֲ��е����֪ʶ���������������Ʒ����������У������������X����ȡ��ֵ�����ǿ���һ������һһ�г����������������������ɢ�������������ɢ����������ķֲ��У�һ���,����ɢ���������X����ȡ��ֵΪx1,x2,.....,xi,......,xn��Xȡÿһ��ֵ xi(i=1,2,......���ĸ���P(��=xi����Pi����Ʊ�Ϊ��ɢ���������X �ĸ��ʷֲ�����Ʒֲ��У�


 ѧ�ڸ�ϰһ��ͨѧϰ�ܶ�Ա��ĩ������ӱ����������ϵ�д�
ѧ�ڸ�ϰһ��ͨѧϰ�ܶ�Ա��ĩ������ӱ����������ϵ�д� â���̸����������������ϵ�д�
â���̸����������������ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����A={x| ![]() ��2x��2}��B={x|ln��x��
��2x��2}��B={x|ln��x�� ![]() ����0}����A�ɣ�RB��=�� ��
����0}����A�ɣ�RB��=�� ��
A.
B.����1�� ![]() ]
]
C.[ ![]() ��1��
��1��
D.����1��1]
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ֱ������ϵxOy �У�F��A��B �ֱ�Ϊ��Բ ![]() ���ҽ��㡢�Ҷ�����϶��㣬��
���ҽ��㡢�Ҷ�����϶��㣬�� ![]()
��1����a��ֵ��
��2������P��0��2����ֱ��l ����Բ��M��N ���㣬��M ��ƽ����x ���ֱ�߽���Բ������һ��Q������NQ ����֤��ֱ��NQ ����һ�����㣮
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��Ʒ��ʦ�趨�ڽ��ܾ�ζ�����ܲ��ԣ�һ��ͨ�����õIJ��Է������£��ó�nƿ�����ͬ��Ʒ�ʲ�ͬ�ľ�����Ʒ����Ҫ���䰴Ʒ������Ϊ����������һ��ʱ�䣬������䵭��֮��������Ʒ����nƿ�ƣ������°�Ʒ������Ϊ�����������Ϊһ�ֲ��ԣ�����һ�ֲ����е����������ƫ��̶ȵĸߵ�Ϊ�����֣� ����n=4���ֱ���a1 �� a2 �� a3 �� a4��ʾ��һ������ʱ����Ϊ1��2��3��4�����־��ڵڶ�������ʱ����ţ�����X=|1��a1|+|2��a2|+|3��a3|+|4��a4|��
��X�Ƕ����������ƫ��̶ȵ�һ��������
����д��X�Ŀ���ֵ���ϣ�
������a1 �� a2 �� a3 �� a4�ȿ��ܵ�Ϊ1��2��3��4�ĸ������У���X�ķֲ��У�
����ijƷ��ʦ����̽��е����ֲ����У�����X��2��
���������еĽ�������������������ĸ��ʣ��ٶ����ֲ������������������Ϊ��Ʒ��ʦ�ľ�ζ��������Σ�˵�����ɣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����f��x��=|x+a|+|x+ ![]() |��a��0��
|��a��0��
��1����a=2ʱ����ʽf��x����3�Ľ⼯��
��2��֤����f��m��+f���� ![]() ����4��
����4��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���涨����P��x��y�������� ![]() ƽ�ƺ�ĵ�ΪQ��x+a��y+b����������
ƽ�ƺ�ĵ�ΪQ��x+a��y+b���������� ![]() ��ͼ������
��ͼ������ ![]() =��j��k����|j|
=��j��k����|j| ![]() ƽ�ƺ��ͼ���Ӧ�ĺ�����
ƽ�ƺ��ͼ���Ӧ�ĺ����� ![]() +1��
+1��
��1���������� ![]() �����ꣻ
�����ꣻ
��2���ڡ�ABC�У���A��B��C���Եı߷ֱ�Ϊa��b��c����֪f��2A��+2cos��B+C��=1�� �����A�Ĵ�С��
����a=6����b+c��ȡֵ��Χ��
���⣺���һС��Ҳ���á����Ҷ�����ϻ�������ʽ����⣮
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij��ÿ������һ�ִ��Ͳ�Ʒ2����ÿ����Ʒ��Ͷ��ɱ�Ϊ1000Ԫ����Ʒ����Ϊһ��Ʒ�ĸ���Ϊ0.5������Ʒ�ĸ���Ϊ0.4��ÿ��һ��Ʒ�ij�����Ϊ5000Ԫ��ÿ������Ʒ�ij�����Ϊ4000Ԫ������Ʒ�������ܴﵽһ��Ʒ�����Ʒ�����ɱ������ջ��⣬ÿ����1����Ʒ�������1000Ԫ����ʧ��
������������������3���У�ǡ������������2����Ʒ��Ϊһ��Ʒ�ĸ��ʣ�
������֪�ó�ij�����������ִ��Ͳ�Ʒ2������1��Ϊһ��Ʒ������1��ҲΪһ��Ʒ�ĸ��ʣ�
������ó�ÿ���������ֲ�Ʒ��������Σ�Ԫ���ķֲ��к�������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�������ͼ��ͼ����������������еĽ��S��ֵ��2016С����ʹ�����S�����ô�жϿ���Ӧ���루 �� 
A.k��10��
B.k��10��
C.k��9��
D.k��9��
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com