
分析 由f(x)=g(x),运用同角的商数关系,求得A的坐标,求出f(x),g(x)的导数,可得切线的斜率,由点斜式方程可得切线的方程,令y=0,可得B,C的坐标,由两点的距离公式计算即可得到所求值.
解答 解:由f(x)=g(x),即cosx=$\sqrt{3}$sinx,x∈(0,$\frac{π}{2}$),
可得tanx=$\frac{\sqrt{3}}{3}$,解得x=$\frac{π}{6}$,
即有A($\frac{π}{6}$,$\frac{\sqrt{3}}{2}$),
由f′(x)=-sinx,g′(x)=$\sqrt{3}$cosx,
可得两曲线在点A处的切线斜率分别为-$\frac{1}{2}$,$\frac{3}{2}$,
可得切线的方程分别为y-$\frac{\sqrt{3}}{2}$=-$\frac{1}{2}$(x-$\frac{π}{6}$),
y-$\frac{\sqrt{3}}{2}$=$\frac{3}{2}$(x-$\frac{π}{6}$),
再令y=0,可得xB=$\frac{π}{6}$+$\sqrt{3}$,xC=$\frac{π}{6}$-$\frac{\sqrt{3}}{3}$,
则|BC|=|xB-xC|=$\frac{4\sqrt{3}}{3}$.
故答案为:$\frac{{4\sqrt{3}}}{3}$.
点评 本题考查导数的运用:求切线的方程,同时考查三角方程的求解方法,直线方程的运用,考查运算能力,属于中档题.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 若样本数据x1,x2,…,xn的均值x=5,则样本数据2x1+1,2x2+1,…,2xn+1的均值为10 | |
| B. | 相关系数r>0,则对应回归直线方程中$\hat b<0$ | |
| C. | 采用系统抽样法从某班按学号抽取5名同学参加活动,学号为5,16,27,38,49的同学均被选出,则该班学生人数可能为60 | |
| D. | 在某项测量中,测量结果X服从正态分布N(1,σ)(σ>0),若X在(0,1)内取值范围概率为0.4,则X在(0,2)内取值的概率为0.8 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 某工厂要安排生产Ⅰ,Ⅱ两种产品,这些产品要在A,B,C,D四种不同的设备上加工,按工艺规定,在一天内,每件产品在各设备上需要加工的时间,及各设备限制最长使用时间如下表:
某工厂要安排生产Ⅰ,Ⅱ两种产品,这些产品要在A,B,C,D四种不同的设备上加工,按工艺规定,在一天内,每件产品在各设备上需要加工的时间,及各设备限制最长使用时间如下表:| 设备 | 产品Ⅰ每件需要加工时间 | 产品Ⅱ每件需要加工时间 | 设备最长使用时间 |
| A | 2小时 | 2小时 | 12小时 |
| B | 1小时 | 2小时 | 8小时 |
| C | 4小时 | 0小时 | 16小时 |
| D | 0小时 | 4小时 | 12小时 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
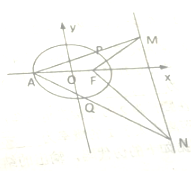 如图,已知椭圆C:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)过点(1,$\frac{3}{2}$),且离心率e=$\frac{1}{2}$,过椭圆右焦点F作互相垂直的两直线与其右准线交于点M、N,A为椭圆的左顶点,连接AM、AN交椭圆于P,Q两点.
如图,已知椭圆C:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)过点(1,$\frac{3}{2}$),且离心率e=$\frac{1}{2}$,过椭圆右焦点F作互相垂直的两直线与其右准线交于点M、N,A为椭圆的左顶点,连接AM、AN交椭圆于P,Q两点.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com