
| A. | 若样本数据x1,x2,…,xn的均值x=5,则样本数据2x1+1,2x2+1,…,2xn+1的均值为10 | |
| B. | 相关系数r>0,则对应回归直线方程中$\hat b<0$ | |
| C. | 采用系统抽样法从某班按学号抽取5名同学参加活动,学号为5,16,27,38,49的同学均被选出,则该班学生人数可能为60 | |
| D. | 在某项测量中,测量结果X服从正态分布N(1,σ)(σ>0),若X在(0,1)内取值范围概率为0.4,则X在(0,2)内取值的概率为0.8 |
分析 A.根据样本平均数之间的关系进行判断.
B.根据相关系数和回归系数的关系,可判断.
C.根据系统抽样的定义进行判断.
D.根据正态分布的定义和概率关系进行判断.
解答 解:A.若样本数据x1,x2,…,xn的均值x=5,则样本数据2x1+1,2x2+1,…,2xn+1的均值为2×5+1=11,故A错误,
B.当变量x,y的线性相关系数r>0时,两个变量有正相关关系,则线性回归方程中的斜率b>0,故B错误,
C.∵学号为5,16,27,38,49的同学均被选出,
∴样本间隔为16-5=11,则对应的人数为11×5=55人,若班学生人数可能为60,则样本间隔为60÷5=12,故C错误,
D.若X在(0,1)内取值范围概率为0.4,
则若X在(1,2)内取值范围概率为0.4,
则X在(0,2)内取值的概率为0.4+0.4=0.8,故D正确,
故选:D
点评 本题考查的知识点是命题的真假判断与应用,此类题型往往综合较多的其它知识点,综合性强,难度中档.


 导学全程练创优训练系列答案
导学全程练创优训练系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $-\frac{1}{3}$ | B. | $\frac{1}{3}$ | C. | $\frac{2}{3}$ | D. | 3 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
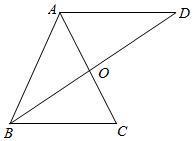 如图,在△ABC中,AB=AC=3,BC=2,B的角平分线交过点A且与BC平行的直线于D,AC与BD交于点O.
如图,在△ABC中,AB=AC=3,BC=2,B的角平分线交过点A且与BC平行的直线于D,AC与BD交于点O.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com