
分析 当x∈[0,3]时,y=f(x)的图象在直线y=x的上方,则围成的平面图形的面积为${∫}_{0}^{3}$(-x2+3x+a)dx,运用定积分运算可得$\frac{9}{2}$+3a,再由条件可得a的范围,求得g(x)的导数,可得切线的斜率,令t=a+1(t≥3),则h(t)=t+$\frac{4}{t}$-5,求出导数,判断单调性可得最小值.
解答 解:当x∈[0,3]时,f(x)-x=-x2+3x+a>0,即有y=f(x)的图象在直线y=x的上方,
则围成的平面图形的面积为${∫}_{0}^{3}$(-x2+3x+a)dx=(-$\frac{1}{3}$x3+$\frac{3}{2}$x2+ax)|${\;}_{0}^{3}$=$\frac{9}{2}$+3a,
由题意可得$\frac{9}{2}$+3a≥$\frac{21}{2}$,解得a≥2.
g(x)=ax-4ln(ax+1)的导数为g′(x)=a-$\frac{4a}{ax+1}$,
可得在点(1,g(1))处的切线斜率为a-$\frac{4a}{a+1}$=(a+1)+$\frac{4}{a+1}$-5,
令t=a+1(t≥3),则h(t)=t+$\frac{4}{t}$-5,
h′(t)=1-$\frac{4}{{t}^{2}}$>0,可得h(t)在[3,+∞)递增,
即有h(t)≥h(3)=3+$\frac{4}{3}$-5=-$\frac{2}{3}$,
则当a=2时,取得最小值-$\frac{2}{3}$.
故答案为:-$\frac{2}{3}$.
点评 本题考查导数的运用:求切线的斜率,同时考查定积分的运用:求面积,考查化简整理的运算能力,属于中档题.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 若样本数据x1,x2,…,xn的均值x=5,则样本数据2x1+1,2x2+1,…,2xn+1的均值为10 | |
| B. | 相关系数r>0,则对应回归直线方程中$\hat b<0$ | |
| C. | 采用系统抽样法从某班按学号抽取5名同学参加活动,学号为5,16,27,38,49的同学均被选出,则该班学生人数可能为60 | |
| D. | 在某项测量中,测量结果X服从正态分布N(1,σ)(σ>0),若X在(0,1)内取值范围概率为0.4,则X在(0,2)内取值的概率为0.8 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
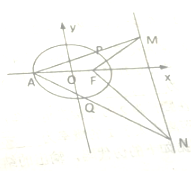 如图,已知椭圆C:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)过点(1,$\frac{3}{2}$),且离心率e=$\frac{1}{2}$,过椭圆右焦点F作互相垂直的两直线与其右准线交于点M、N,A为椭圆的左顶点,连接AM、AN交椭圆于P,Q两点.
如图,已知椭圆C:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)过点(1,$\frac{3}{2}$),且离心率e=$\frac{1}{2}$,过椭圆右焦点F作互相垂直的两直线与其右准线交于点M、N,A为椭圆的左顶点,连接AM、AN交椭圆于P,Q两点.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com