
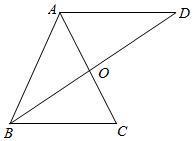
 如图,在△ABC中,AB=AC=3,BC=2,B的角平分线交过点A且与BC平行的直线于D,AC与BD交于点O.
如图,在△ABC中,AB=AC=3,BC=2,B的角平分线交过点A且与BC平行的直线于D,AC与BD交于点O.分析 (1)运用三角形的内角平分线定理和三角形的面积公式,计算即可得到所求值;
(2)由等腰三角形的定义和平行线的性质,结合诱导公式可得sin∠BAD=sinC,运用余弦定理和同角的平方关系,计算即可得到所求值.
解答 解:(1)BD为∠ABC的平分线,
由角平分线定理知:$\frac{OA}{OC}=\frac{AB}{BC}=\frac{3}{2}$,
即有$\frac{{{S_{△OAB}}}}{{{S_{△OBC}}}}=\frac{OA}{OC}=\frac{3}{2}$;
(2)由AD∥BC且AB=AC,
可得∠ABC=∠ACB=∠CAD,
即有sin∠BAD=sin(∠BAC+∠CAD)=sin(∠BAC+∠ABC)=sinC,
在△ABC中,AB=AC=3,BC=2,
可得$cosC=\frac{{A{C^2}+B{C^2}-A{B^2}}}{2•AC•BC}=\frac{1}{3}$,
即有sinC=$\sqrt{1-co{s}^{2}C}$=$\frac{2\sqrt{2}}{3}$,
故sin∠BAD的值为$\frac{{2\sqrt{2}}}{3}$.
点评 本题考查角平分线定理和余弦定理的运用,同时考查三角函数的诱导公式及同角的平方关系,考查运算能力,属于中档题.


科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 若样本数据x1,x2,…,xn的均值x=5,则样本数据2x1+1,2x2+1,…,2xn+1的均值为10 | |
| B. | 相关系数r>0,则对应回归直线方程中$\hat b<0$ | |
| C. | 采用系统抽样法从某班按学号抽取5名同学参加活动,学号为5,16,27,38,49的同学均被选出,则该班学生人数可能为60 | |
| D. | 在某项测量中,测量结果X服从正态分布N(1,σ)(σ>0),若X在(0,1)内取值范围概率为0.4,则X在(0,2)内取值的概率为0.8 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com