

���� ��1����ֱ��ͼ�����ʿɵã�0.002+0.0095+0.011+0.0125+x+0.005+0.0025����20=1���ⷽ�̿ɵã�
��2����ֱ��ͼ������Ϊ��߾����϶˵��е�ɵã��ɵ���λ����[220��240���ڣ�����λ��Ϊa���ⷽ�̣�0.002+0.0095++0.011����20+0.0125����a-220��=0.5�ɵã�
��3���ɵø��ε��û��ֱ�Ϊ25��15��10��5���ɵó�ȡ�������ɵ�Ҫ��ȡ�Ļ�����
��� �⣺��1����ֱ��ͼ�����ʿɵã�0.002+0.0095+0.011+0.0125+x+0.005+0.0025����20=1��
�ⷽ�̿ɵ�x=0.0075����ֱ��ͼ��x��ֵΪ0.0075��
��2����ƽ���õ�����������$\frac{220+240}{2}$=230��
�ߣ�0.002+0.0095+0.011����20=0.45��0.5��
����ƽ���õ�������λ����[220��240���ڣ�
����λ��Ϊa���ɣ�0.002+0.0095+0.011����20+0.0125����a-220��=0.5�ɵ�a=224��
����ƽ���õ�������λ��Ϊ224��
��3����ƽ���õ���Ϊ[220��240�����û���0.0125��20��100=25��
��ƽ���õ���Ϊ[240��260�����û���0.0075��20��100=15��
��ƽ���õ���Ϊ[260��280�����û���0.005��20��100=10��
��ƽ���õ���Ϊ[280��300�����û���0.0025��20��100=5��
���ȡ����Ϊ$\frac{11}{25+15+10+5}$=$\frac{1}{5}$��
����ƽ���õ�����[220��240�����û���Ӧ��ȡ25��$\frac{1}{5}$=5����
���� ���⿼��Ƶ�ʷֲ�ֱ��ͼ���漰��������λ���Լ��ֲ�������������⣮



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | $\frac{1}{14}$ | B�� | $\frac{1}{16}$ | C�� | $\frac{1}{18}$ | D�� | $\frac{1}{20}$ |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 2 | B�� | 3 | C�� | 4 | D�� | 9 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
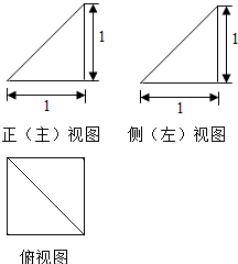
| A�� | 1 | B�� | $\sqrt{2}$ | C�� | $\sqrt{3}$ | D�� | 2 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | $\sqrt{2}$ | B�� | 2 | C�� | 2$\sqrt{2}$ | D�� | 4 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
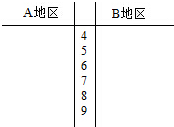 ij��˾Ϊ�˽��û������Ʒ������ȣ���A��B�������ֱ����������20���û����õ��û��Բ�Ʒ��������������£�
ij��˾Ϊ�˽��û������Ʒ������ȣ���A��B�������ֱ����������20���û����õ��û��Բ�Ʒ��������������£�| ��������� | ����70�� | 70�ֵ�89�� | ������90�� |
| ����ȵȼ� | ������ | ���� | �dz����� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 7 | B�� | 6 | C�� | 5 | D�� | 4 |
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com