
分析 (1)设f(x)=ax2+bx+c,由f(0)=8可求c,由f(x+1)-f(x)=-2x+1可构造关于a,b的方程组,可求解.
(2)结合对数函数的单调性以及一元二次函数的性质进行求解即可.
解答 解:(1)设f(x)=ax2+bx+c,
∵f(0)=8,∴c=8
又f(x+1)=a(x+1)2+b(x+1)+c,
∵f(x+1)-f(x)=-2x+1
∴a(x+1)2+b(x+1)+c-(ax2+bx+c)=2ax+a+b=-2x+1,
∴$\left\{\begin{array}{l}2a=-2\\ a+b=1\end{array}\right.$,
∴a=-1,b=2
∴f(x)=-x2+2x+8.
(2)∵f(x)=-x2+2x+8=-(x-1)2+9,
∴由y=log3f(x)得0<f(x)≤9,
则y=log3f(x)≤log39=2,
即函数的值域为(-∞,2].
点评 本题主要考查函数解析式以及函数值域的求解,根据一元二次函数的性质,利用待定系数法是解决本题的关键.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:选择题
| A. | 120 | B. | 240 | C. | 107 | D. | 360 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
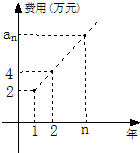 某公司今年年初用25万元引进一种新的设备,投入设备后每年收益为21万元.该公司第n年需要支付设备的维修和工人工资等费用an的信息如图.
某公司今年年初用25万元引进一种新的设备,投入设备后每年收益为21万元.该公司第n年需要支付设备的维修和工人工资等费用an的信息如图.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com