
分析 (Ⅰ)先求导,再构造函数,根据导数和函数的单调性的关系即可判断f(x)在(0,1)上的单调性,
(Ⅱ)先求导,设h'(x0)=0,则x0∈(0,1),则h(x)在(0,x0)上单调递减,在(x0,+∞)上单调递增,由(Ⅰ)知$\left.\begin{array}{l}f({x_1})<f({x_0})\\ f({x_2})>f({x_0})\end{array}\right\}⇒\left\{\begin{array}{l}h({x_1})>f({x_0})(x_1^2-{x_1})\\ h({x_2})<f({x_0})(x_2^2-{x_2})\end{array}\right.$,即可证明x1+x2>1.
解答 解:(Ⅰ)$f'(x)=\frac{x-1-lnx}{{{{(x-1)}^2}}}$,
设g(x)=x-1-lnx,
则$g'(x)=1-\frac{1}{x}$,
∴当x∈(0,1)时,g'(x)<0,
∴g(x)>g(1)=0,
∴f'(x)>0,
∴f(x)在(0,1)上单调递增.
(Ⅱ)h(x)=x2lnx-ax2+ax(a<0),
∴h'(x)=2xlnx+x-2ax+a,
∴h''(x)=2lnx-2a+3,
∴h''(x)在(0,+∞)上单调递增,
当x→0时,h''(x)<0,h''(1)=3-2a>0,
∴必存在α∈(0,1),使得h''(x)=0,即2lnα-2a+3=0,
∴h'(x)在(0,α)上单调递减,在(α,+∞)上单调递增,
又h'(α)=a-2α<0,h'(1)=1-a>0,
设h'(x0)=0,则x0∈(0,1),
∴h(x)在(0,x0)上单调递减,在(x0,+∞)上单调递增,
又h(1)=0,不妨设x1<x2,则0<x1<x0,x0<x2<1,
由(Ⅰ)知$\left.\begin{array}{l}f({x_1})<f({x_0})\\ f({x_2})>f({x_0})\end{array}\right\}⇒\left\{\begin{array}{l}h({x_1})>f({x_0})(x_1^2-{x_1})\\ h({x_2})<f({x_0})(x_2^2-{x_2})\end{array}\right.$,
∴$f({x_0})(x_2^2-{x_2})>h({x_2})=h({x_1})>f({x_0})(x_1^2-{x_1})$,
∴$(x_2^2-{x_2})-(x_1^2-{x_1})=({x_2}-{x_1})({x_2}+{x_1}-1)>0$,
∴x1+x2>1.
点评 本题考查了函数和单调性和导数的关系以及方程的根与1的关系,考查了分析问题,解决问题的能力,属于中档题.


科目:高中数学 来源: 题型:选择题
| A. | 在回归分析中,变量间的关系若是非确定性关系,那么因变量不能由自变量唯一确定 | |
| B. | 线性相关系数可以是正的也可以是负的 | |
| C. | 在回归分析中,如果r2=1或r=±1,说明x与y之间完全线性相关 | |
| D. | 样本相关系数r∈(-1,1) |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
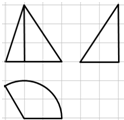
| A. | $\frac{2π}{3}$ | B. | $\frac{4π}{3}$ | C. | $\frac{14π}{3}$ | D. | $\frac{16π}{9}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $-\frac{1}{5}+\frac{2}{5}i$ | B. | $-\frac{1}{5}-\frac{2}{5}i$ | C. | $\frac{1}{5}+\frac{2}{5}i$ | D. | $\frac{1}{5}-\frac{2}{5}i$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | g(m)<0<f(n) | B. | f(n)<0<g(m) | C. | 0<g(m)<f(n) | D. | f(n)<g(m)<0 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 3×4=12种 | B. | 4×3×2=24种 | C. | 43=64种 | D. | 34=81种 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com