
分析 (1)根据等比数列前n项和公式,$\frac{{a}_{3}}{{q}^{2}}$+$\frac{{a}_{3}}{q}$+a3=$\frac{7}{4}$.整理求得q及a1的值,即求得an=$\frac{1}{2n-1}$,Sn=2-$\frac{1}{2n-1}$<2,有$\frac{Sn+Sn+2}{2}$=2-$\frac{1}{2n}$-$\frac{1}{2n+2}$<2-$\frac{1}{2n}$=Sn+1,且Sn<2,即可证明{Sn}是Ω数列;
(2)由an+1-an<0,故数列{an}单调递减;当n=1,2时,an+1-an>0,即a1<a2<a3,则数列{bn}中的最大项是a3=7,即可求得M≥7;
(3)采用反证法,假设存在常数n∈N*,使得a${\;}_{n_0}}$>a${\;}_{{n_0}+1}}$,∵{an}是Ω数列,得a${\;}_{{n_0}+1}}$-a${\;}_{n_0}}$≤1,${a}_{{n}_{0}+2}$-a${\;}_{{n_0}+1}}$≤-1,采用累加法${a}_{{n}_{0}+m}$-${a}_{{n}_{0}}$≤-m,
由当m取${a}_{{n}_{0}}$时,${a}_{{n}_{0}+m}$≤0与an∈N*矛盾,不存在常数n0∈N*,使得a${\;}_{n_0}}$>a${\;}_{{n_0}+1}}$.
解答 解:(1)证明∵{an}是各项正数的等比数列,Sn是其前n项和,a3=$\frac{1}{4}$,S3=$\frac{7}{4}$,
设其公比为q>0,
∴$\frac{{a}_{3}}{{q}^{2}}$+$\frac{{a}_{3}}{q}$+a3=$\frac{7}{4}$.整理得6q2-q-1=0,
解得q=$\frac{1}{2}$,q=-$\frac{1}{3}$(舍去).
∴a1=1,…(3分)
an=$\frac{1}{2n-1}$,Sn=2-$\frac{1}{2n-1}$<2,…(4分)
对任意的n∈N*,有$\frac{Sn+Sn+2}{2}$=2-$\frac{1}{2n}$-$\frac{1}{2n+2}$<2-$\frac{1}{2n}$=Sn+1,且Sn<2,
故{Sn}是Ω数列.…(5分)
(2)∵an+1-an=5-2n,…(7分)
∴当n≥3,an+1-an<0,故数列{an}单调递减;
当n=1,2时,an+1-an>0,即a1<a2<a3,
则数列{bn}中的最大项是a3=7,
所以M≥7.…(9分)
(3)证明:假设存在常数n∈N*,使得a${\;}_{n_0}}$>a${\;}_{{n_0}+1}}$,即a${\;}_{{n_0}+1}}$-a${\;}_{n_0}}$<0;…(10分)
∵{an}是各项均为正整数的数列,所以a${\;}_{{n_0}+1}}$-a${\;}_{n_0}}$≤1;
又∵{an}是Ω数列,所以${a}_{{n}_{0}}$+${a}_{{n}_{0}+2}$≤2a${\;}_{{n_0}+1}}$,
即${a}_{{n}_{0}+2}$-a${\;}_{{n_0}+1}}$≤a${\;}_{{n_0}+1}}$-a${\;}_{n_0}}$≤-1,得${a}_{{n}_{0}+2}$-a${\;}_{{n_0}+1}}$≤-1,…(12分)
以此类推,${a}_{{n}_{0}+k}$-${a}_{{n}_{0}+k-1}$≤-1,①(n∈N*,);
将①中k赋值1,2,3…m,累加可得${a}_{{n}_{0}+m}$-${a}_{{n}_{0}}$≤-m,
即${a}_{{n}_{0}+m}$≤${a}_{{n}_{0}}$-m;…(14分)
当m取${a}_{{n}_{0}}$时,${a}_{{n}_{0}+m}$≤0与an∈N*矛盾;
∴假设错误,不存在常数n0∈N*,使得${a}_{{n}_{0}}$>${a}_{{n}_{0}+1}$.…(16分)
点评 本题考查数列的新定义,考查等比数列前n项和公式,考查“累加法”及“反证法”,考查学生分析问题及解决问题得能力,属于中档题.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:选择题
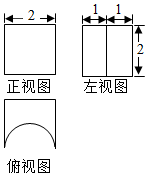 某几何体的三视图如图所示,其中俯视图下半部分是半径为1的半圆,则该几何体的表面积是( )
某几何体的三视图如图所示,其中俯视图下半部分是半径为1的半圆,则该几何体的表面积是( )| A. | 20+2π | B. | 20+π | C. | 20-2π | D. | 20-π |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
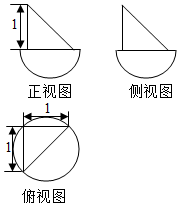
| A. | $\frac{2π}{3}$+$\frac{1}{6}$ | B. | $\frac{π}{3}$+$\frac{1}{3}$ | C. | $\frac{π}{3}$+$\frac{1}{6}$ | D. | $\frac{\sqrt{2}π}{6}$+$\frac{1}{6}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (-∞,2] | B. | (-∞,0] | C. | [0,+∞) | D. | [2,+∞) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (0,$\frac{2}{e}$) | B. | ($\frac{1}{e}$,+∞) | C. | (e,+∞) | D. | (-∞,$\frac{1}{e}$] |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | a>b>c | B. | b>a>c | C. | a>c>b | D. | c>a>b |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com