
���� ��1��������֪��$y=��{4+\frac{20}{p}}��p-x-��{10+2p}��$����$p=3-\frac{2}{x+1}$���뻯�ɵó���
��2��y��=$-\frac{��x+3����x-1��}{��x+1��^{2}}$����a�������ۣ����õ����о������ĵ����Լ��ɵó���
��� �⣺��1��������֪��$y=��{4+\frac{20}{p}}��p-x-��{10+2p}��$����$p=3-\frac{2}{x+1}$���뻯��ã�$y=16-\frac{4}{x+1}-x��{0��x��a}��$��
��2��$y'=-1-\frac{-4}{{{{��{x+1}��}^2}}}=\frac{{-{{��{x+1}��}^2}+4}}{{{{��{x+1}��}^2}}}=-\frac{{{x^2}+2x-3}}{{{{��{x+1}��}^2}}}=-\frac{{��{x+3}����{x-1}��}}{{{{��{x+1}��}^2}}}$��
�ٵ�a��1ʱ��x�ʣ�0��1��ʱ��y'��0�����Ժ���$y=16-x-\frac{4}{x+1}$�ڣ�0��1���ϵ���������
x�ʣ�1��a��ʱ��y'��0�����Ժ���$y=16-x-\frac{4}{x+1}$�ڣ�1��a���ϵ����ݼ���
���������Ͷ�� 1��Ԫʱ�����ҵ��������
�ڵ�a��1ʱ����Ϊ����$y=16-x-\frac{4}{x+1}$�ڣ�0��1���ϵ���������$y=16-x-\frac{4}{x+1}$��[0��a]�ϵ���������
����x=aʱ�����������ֵ������������Ͷ��a��Ԫʱ�����ҵ��������
������������ a��1ʱ����������Ͷ�� 1��Ԫ�����ҵ��������a��1ʱ����������Ͷ��a��Ԫ�����ҵ��������
���� ���⿼�������õ����о������ĵ����ԡ���ֵ����ֵ�������˷������۷�����������������������������е��⣮


 ��ѧ����ͬ����ϰϵ�д�
��ѧ����ͬ����ϰϵ�д� ��ǰ�κ�ͬ����ϰϵ�д�
��ǰ�κ�ͬ����ϰϵ�д� ����С��ҵϵ�д�
����С��ҵϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
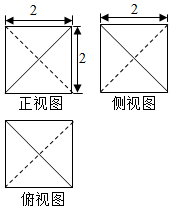 ij�����������ͼ��ͼ��ʾ����������������ǣ�������
ij�����������ͼ��ͼ��ʾ����������������ǣ�������| A�� | 2 | B�� | 8 | C�� | $\frac{8}{3}$ | D�� | $\frac{16}{3}$ |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | sin��2��x-$\frac{��}{2}$�� | B�� | sin��$\frac{��}{2}$x-$\frac{��}{2}$�� | C�� | sin����x-$\frac{��}{2}$�� | D�� | sin����x+$\frac{��}{2}$�� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
 ij��������һ��ƽ���ȥһ���ֺ����õļ����������ͼ��ͼ��ʾ�����и���ͼ�DZ߳�Ϊ2���������Σ����ȥ���ֺ�ʣ�ಿ�ֵ����֮��Ϊ��������
ij��������һ��ƽ���ȥһ���ֺ����õļ����������ͼ��ͼ��ʾ�����и���ͼ�DZ߳�Ϊ2���������Σ����ȥ���ֺ�ʣ�ಿ�ֵ����֮��Ϊ��������| A�� | $\frac{10}{33}$ | B�� | $\frac{13}{36}$ | C�� | $\frac{13}{23}$ | D�� | $\frac{23}{33}$ |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | $\frac{20}{3}��$ | B�� | $\frac{25}{3}��$ | C�� | $\frac{28}{3}��$ | D�� | $\frac{32}{3}��$ |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | ��4��8�� | B�� | [4��9�� | C�� | ��-�ޣ�4] | D�� | ��-�ޣ�9�� |
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com