
分析 (1)根据函数奇偶性的定义进行判断即可,
(2)根据函数单调性的定义,利用定义法进行证明,
(3)根据函数奇偶性和单调性之间的关系将不等式进行转化求解即可.
解答 解:(1)由2x+1>1得函数的定义域为R,
又f(-x)+f(x)=$\frac{1}{{2}^{-x}+1}$-$\frac{1}{2}$+$\frac{1}{{2}^{x}+1}$-$\frac{1}{2}$=$\frac{{2}^{x}}{{2}^{x}+1}$+$\frac{1}{{2}^{x}+1}$-1=1-1=0.
则f(-x)=-f(x),
故f(x)为奇函数.
(2)f(x)为R上的减函数 证明如下:
任取x1<x2,则f(x1)-f(x2)=$\frac{1}{{2}^{{x}_{1}}+1}$-$\frac{1}{2}$-$\frac{1}{{2}^{{x}_{2}}+1}$+$\frac{1}{2}$=$\frac{1}{{2}^{{x}_{1}}+1}$-$\frac{1}{{2}^{{x}_{2}}+1}$=$\frac{{2}^{{x}_{2}}-{2}^{{x}_{1}}}{({2}^{{x}_{1}}+1)({2}^{{x}_{1}}+1)}$,
∵x1<x2,∴2${\;}^{{x}_{1}}$<2${\;}^{{x}_{2}}$,
则f(x1)-f(x2)=$\frac{{2}^{{x}_{2}}-{2}^{{x}_{1}}}{({2}^{{x}_{1}}+1)({2}^{{x}_{1}}+1)}$>0,
∴f(x1)>f(x2),
故f(x)为R上的减函数.
(3)由(1)(2)知f(x)在R上是奇函数且单调递减,
由f(f(x))+f($\frac{3}{8}$)<0得f(f(x))<-f($\frac{3}{8}$)=f(-$\frac{3}{8}$),
则f(x)>-$\frac{3}{8}$,
∴$\frac{1}{{2}^{x}+1}$-$\frac{1}{2}$>-$\frac{3}{8}$,
即2x<7,得x<log27,
故不等式的解集为(-∞,log27).
点评 本题主要函数奇偶性和单调性判断,利用函数奇偶性和单调性的定义是解决本题的关键.考查学生的转化能力.


 初中学业考试导与练系列答案
初中学业考试导与练系列答案科目:高中数学 来源: 题型:选择题
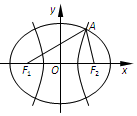 如图,F1,F2是双曲线C1:x2-$\frac{y^2}{3}$=1与椭圆C2的公共焦点,点A是C1,C2在第一象限的公共点,若|F1F2|=|F1A|,则C2的离心率是( )
如图,F1,F2是双曲线C1:x2-$\frac{y^2}{3}$=1与椭圆C2的公共焦点,点A是C1,C2在第一象限的公共点,若|F1F2|=|F1A|,则C2的离心率是( )| A. | $\frac{1}{3}$ | B. | $\frac{2}{3}$ | C. | $\frac{2}{3}$或$\frac{2}{5}$ | D. | $\frac{2}{5}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | “存在x0∈R,x02+sinx0+ex0<1”的否定是“不存在x0∈R,x02+sinx0+ex0<1” | |
| B. | 在△ABC中,“AB2+AC2>BC2”是“△ABC为锐角三角形”的充分不必要条件 | |
| C. | 任意x∈N,3x>1 | |
| D. | 存在x0∈(0,$\frac{π}{2}$),sinx0+cosx0=tanx0 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com