
| A. | “存在x0∈R,x02+sinx0+ex0<1”的否定是“不存在x0∈R,x02+sinx0+ex0<1” | |
| B. | 在△ABC中,“AB2+AC2>BC2”是“△ABC为锐角三角形”的充分不必要条件 | |
| C. | 任意x∈N,3x>1 | |
| D. | 存在x0∈(0,$\frac{π}{2}$),sinx0+cosx0=tanx0 |
分析 直接写出命题的否定判断A;由充分必要条件的判定方法判断B;举例说明C错误;利用辅助角公式化积,结合三角函数的图象判断D.
解答 解:对于A,“存在x0∈R,x02+sinx0+ex0<1”的否定是“存在x0∈R,x02+sinx0+ex0≥1”,故A为假命题;
对于B,∵AB2+AC2>BC2?$\frac{A{B}^{2}+A{C}^{2}-B{C}^{2}}{2AB•AC}>0$,即cosA>0,
∵0<A<π,故A为锐角,但未必有△ABC为锐角三角形;反之,若△ABC为锐角三角形,则0<A<$\frac{π}{2}$,故cosA>0,即AB2+AC2>BC2,
∴“AB2+AC2>BC2”是“△ABC为锐角三角形”的必要不充分条件,故B为假命题;
对于C,当x=0时,30=1,故C为假命题;
对于D,∵sinx+cosx=$\sqrt{2}sin(x+\frac{π}{4})$,故命题转化为存在x0∈(0,$\frac{π}{2}$),$\sqrt{2}sin({x}_{0}+\frac{π}{4})=tan{x}_{0}$,
在同一直角坐标系内分别作出y=$\sqrt{2}sin(x+\frac{π}{4})$与y=tanx在[0,$\frac{π}{2}$]上的图象如图:
可知y=$\sqrt{2}sin(x+\frac{π}{4})$与y=tanx在[0,$\frac{π}{2}$]上必有交点,即存在x0∈(0,$\frac{π}{2}$),$\sqrt{2}sin({x}_{0}+\frac{π}{4})=tan{x}_{0}$,
故D为真命题.
故选:D.
点评 本题考查命题的真假判断与应用,考查了充分必要条件的判定方法,考查三角函数的图象和性质,是中档题.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 2 | B. | 5 | C. | 8 | D. | 10 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
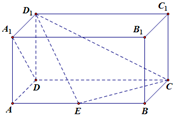 如图,在长方体ABCD-A1B1C1D1中,AD=AA1=1,AB=2,点E在棱AB上.
如图,在长方体ABCD-A1B1C1D1中,AD=AA1=1,AB=2,点E在棱AB上.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com