
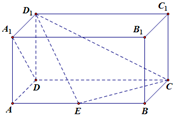
 如图,在长方体ABCD-A1B1C1D1中,AD=AA1=1,AB=2,点E在棱AB上.
如图,在长方体ABCD-A1B1C1D1中,AD=AA1=1,AB=2,点E在棱AB上.分析 (1)连结AD1,由题意可知AD1⊥A1D,再由AB⊥平面AA1D1D,得AB⊥A1D,由线面垂直的判定可得A1D⊥面AED1,从而得D1E⊥A1D;
(2)假设存在这样的点E,且AE=x,则BE=2-x,由${V_{B-CE{D_1}}}={V_{{D_1}-BCE}}$,结合棱锥体积公式列式求得x值.
解答 (1)证明:连结AD1.由AA1D1D是正方形知AD1⊥A1D.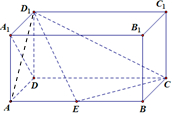
∵AB⊥平面AA1D1D,∴AB⊥A1D,且AB∩AD1=A,
∴A1D⊥面AED1,又D1E?面AED1,∴D1E⊥A1D;
(2)解:假设存在这样的点E,且AE=x,则BE=2-x,${S_{△BCE}}=\frac{1}{2}BE•BC=\frac{1}{2}(2-x)$,
又${V_{B-CE{D_1}}}={V_{{D_1}-BCE}}$,
即${V_{{D_1}-BCE}}=\frac{1}{9}$,即$\frac{1}{3}{S_{△BCE}}•D{D_1}=\frac{1}{9}$,得$\frac{1}{2}(2-x)=\frac{1}{3}$,从而$x=\frac{4}{3}$.
即存在这样的点E,使得${V_{B-CE{D_1}}}=\frac{1}{9}$,此时$AE=\frac{4}{3}$.
点评 本题考查空间中直线与直线的位置关系,考查了线面垂直的判断,训练了等积法求多面体的体积,是中档题.


 培优三好生系列答案
培优三好生系列答案科目:高中数学 来源: 题型:选择题
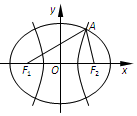 如图,F1,F2是双曲线C1:x2-$\frac{y^2}{3}$=1与椭圆C2的公共焦点,点A是C1,C2在第一象限的公共点,若|F1F2|=|F1A|,则C2的离心率是( )
如图,F1,F2是双曲线C1:x2-$\frac{y^2}{3}$=1与椭圆C2的公共焦点,点A是C1,C2在第一象限的公共点,若|F1F2|=|F1A|,则C2的离心率是( )| A. | $\frac{1}{3}$ | B. | $\frac{2}{3}$ | C. | $\frac{2}{3}$或$\frac{2}{5}$ | D. | $\frac{2}{5}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | “存在x0∈R,x02+sinx0+ex0<1”的否定是“不存在x0∈R,x02+sinx0+ex0<1” | |
| B. | 在△ABC中,“AB2+AC2>BC2”是“△ABC为锐角三角形”的充分不必要条件 | |
| C. | 任意x∈N,3x>1 | |
| D. | 存在x0∈(0,$\frac{π}{2}$),sinx0+cosx0=tanx0 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com