
分析 若对于任意的x1,x2∈R,都满足条件$\frac{{f({x_2})-f({x_1})}}{{{x_2}-{x_1}}}>0({x_1}≠{x_2})$成立,则函数$f(x)=\left\{\begin{array}{l}(a-1)x+3a-4,x≤0\\{a^x},x>0\end{array}\right.$在R上为增函数,里面可得答案.
解答 解:若对于任意的x1,x2∈R,都满足条件$\frac{{f({x_2})-f({x_1})}}{{{x_2}-{x_1}}}>0({x_1}≠{x_2})$成立,
则函数$f(x)=\left\{\begin{array}{l}(a-1)x+3a-4,x≤0\\{a^x},x>0\end{array}\right.$在R上为增函数,
故$\left\{\begin{array}{l}a-1>0\\ a>1\\ 3a-4≤1\end{array}\right.$,
解得:$1<a≤\frac{5}{3}$,
故答案为:$1<a≤\frac{5}{3}$
点评 本题考查的知识点是恒成立问题,分段函数的单调性,难度中档.


 小学课时作业全通练案系列答案
小学课时作业全通练案系列答案 金版课堂课时训练系列答案
金版课堂课时训练系列答案 单元全能练考卷系列答案
单元全能练考卷系列答案 新黄冈兵法密卷系列答案
新黄冈兵法密卷系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 2 | B. | 5 | C. | 8 | D. | 10 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
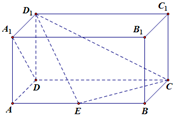 如图,在长方体ABCD-A1B1C1D1中,AD=AA1=1,AB=2,点E在棱AB上.
如图,在长方体ABCD-A1B1C1D1中,AD=AA1=1,AB=2,点E在棱AB上.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 2 | B. | $\sqrt{5}$ | C. | $\sqrt{3}$ | D. | $\frac{\sqrt{5}}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com