
分析 (1)直接利用函数f(x)=x-sinx,数列{an}满足an+1=f(an),可得a3-a2<0,从而可得结论;
(2)证题的关键是n=k+1时,结论成立,利用函数是(0,1)上的单调递增函数即可;
(3)设函数$g(x)=sinx-x+\frac{1}{6}{x^3},0<x<1$,求导判断函数的单调性,即可证明.
解答 解:(1)因为0<x<1时,f'(x)=1-cosx>0所以f(x)在(0,1)上是增函数,
(2)证明:
①当n=1时,由已知,结论成立.
②假设当n=k时结论成立,即0<ak<1,
因为f(x)在(0,1)上是增函数,又f(x)在[0,1]上图象不间断,
从而f(0)<f(ak)<f(1),即0<ak+1<1-sin1<1,
故当n=k+1时,结论成立.
由①②可知,0<an<1对一切正整数都成立.
(2)设函数$g(x)=sinx-x+\frac{1}{6}{x^3},0<x<1$,由(1)可知,当0<x<1时,sinx<x.
从而$g'(x)=cosx-1+\frac{x^2}{2}=-2{sin^2}\frac{x}{2}+\frac{x^2}{2}>-2{(\frac{x}{2})^2}+\frac{x^2}{2}=0$,所以g(x)在(0,1)上是增函数.
又g(0)=0,所以当0<x<1时,g(x)>0成立.
于是g(an)>0,即$sin{a_n}-{a_n}+\frac{1}{6}{a_n}^3>0$,故${a_{n+1}}<\frac{1}{6}a_n^3$.
点评 本题考查数学归纳法,考查学生分析解决问题的能力,掌握数学归纳法的证题步骤是关键.


科目:高中数学 来源: 题型:解答题
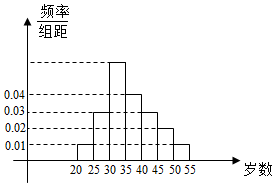 某中学利用周末组织教职员工进行了一次秋季登山健身的活动,有N人参加,现将所有参加者按年龄情况分为[20,25),[25,30),[30,35),[35,40),[40,45),[45,50),[50,55)等七组,其频率分布直方图如下所示.已知[35,40)这组的参加者是8人.
某中学利用周末组织教职员工进行了一次秋季登山健身的活动,有N人参加,现将所有参加者按年龄情况分为[20,25),[25,30),[30,35),[35,40),[40,45),[45,50),[50,55)等七组,其频率分布直方图如下所示.已知[35,40)这组的参加者是8人.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
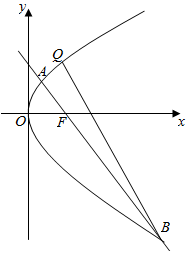 设抛物线y2=2px(p>0)的焦点F,已知抛物线上一点Q,其纵坐标为4,且|QF|=4.
设抛物线y2=2px(p>0)的焦点F,已知抛物线上一点Q,其纵坐标为4,且|QF|=4.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{2\sqrt{5}}{5}$ | B. | $\frac{4}{5}$ | C. | $\frac{4\sqrt{5}}{5}$ | D. | $\frac{16}{5}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com