
分析 (1)把a=0代入函数解析式,求得导函数,由导函数的零点得到函数的单调性,由此求得函数的最小值;
(2)①由f(x)有两个极值点,可得导函数有两个不同的零点,进一步转化为$\frac{1+lnx}{x}=a$有两个不同解,令φ(x)=$\frac{1+lnx}{x}$,利用导数求其最大值,再结合φ($\frac{1}{e}$)=0,可得a∈(0,1),且x1∈($\frac{1}{e},1$);
②由①可得,1+lnx1=ax1,f(x1)=${x}_{1}ln{x}_{1}-\frac{1}{2}a{{x}_{1}}^{2}$,消去a可得$f({x}_{1})={x}_{1}ln{x}_{1}-\frac{1}{2}{x}_{1}(1+ln{x}_{1})=\frac{1}{2}$(x1lnx1-x1),x1∈$(\frac{1}{e},1)$,构造函数g(x)=xlnx-x,x∈($\frac{1}{e},1$),利用导数求得g(x)的单调性,即可证得$f({x}_{1})<f(\frac{1}{e})=-\frac{1}{e}$;由①可得lnx1=ax1-1,lnx2=ax2-1,联立两式可得$ln{x}_{1}{x}_{2}=\frac{(ln{x}_{1}-ln{x}_{2})({x}_{1}+{x}_{2})}{{x}_{1}-{x}_{2}}-2$=$\frac{ln\frac{{x}_{1}}{{x}_{2}}(1+\frac{{x}_{1}}{{x}_{2}})}{\frac{{x}_{1}}{{x}_{2}}-1}-2$,令t=$\frac{{x}_{1}}{{x}_{2}}∈(0,1)$,构造函数$h(t)=\frac{(t+1)lnt}{t-1}-2$,经过三次求导得答案.
解答 解:(1)当a=0时,f(x)=xlnx,f′(x)=1+lnx,当x∈(0,$\frac{1}{e}$)时,f′(x)<0,
当x∈($\frac{1}{e},+∞$)时,f′(x)>0,
∴$f(x)_{min}=f(\frac{1}{e})=-\frac{1}{e}$;
(2)①f′(x)=1+lnx-ax,由于f(x)有两个极值点,可得1+lnx-ax=0有两个不同解,即$\frac{1+lnx}{x}=a$有两个不同解,
令φ(x)=$\frac{1+lnx}{x}$,则φ′(x)=$\frac{-lnx}{{x}^{2}}$,φ′(1)=0,当x∈(0,1)时,φ′(x)>0,当x∈(1,+∞)时,φ′(x)<0,
∴φ(x)max=φ(1)=1,且φ($\frac{1}{e}$)=0,由数形结合可得a∈(0,1),且x1∈($\frac{1}{e},1$),
②由①可得,1+lnx1=ax1,f(x1)=${x}_{1}ln{x}_{1}-\frac{1}{2}a{{x}_{1}}^{2}$,消去a可得
$f({x}_{1})={x}_{1}ln{x}_{1}-\frac{1}{2}{x}_{1}(1+ln{x}_{1})=\frac{1}{2}$(x1lnx1-x1),x1∈$(\frac{1}{e},1)$,构造函数g(x)=xlnx-x,x∈($\frac{1}{e},1$),
g′(x)=lnx<0,∴g(x)在($\frac{1}{e},1$)上单调递减,则$f({x}_{1})<f(\frac{1}{e})=-\frac{1}{e}$,
再证x1x2>1:由①可得lnx1=ax1-1,lnx2=ax2-1,将两式相加可得lnx1x2=a(x1+x2)-2,
两式相减可得lnx1-lnx2=a(x1-x2),即$a=\frac{ln{x}_{1}-ln{x}_{2}}{{x}_{1}-{x}_{2}}$,代入lnx1x2=a(x1+x2)-2,可得
$ln{x}_{1}{x}_{2}=\frac{(ln{x}_{1}-ln{x}_{2})({x}_{1}+{x}_{2})}{{x}_{1}-{x}_{2}}-2$=$\frac{ln\frac{{x}_{1}}{{x}_{2}}(1+\frac{{x}_{1}}{{x}_{2}})}{\frac{{x}_{1}}{{x}_{2}}-1}-2$,令t=$\frac{{x}_{1}}{{x}_{2}}∈(0,1)$,
构造函数$h(t)=\frac{(t+1)lnt}{t-1}-2$,h′(t)=$\frac{{t}^{2}-1-2tlnt}{t(t-1)^{2}}$,再令k(t)=t2-1-2tlnt,t∈(0,1),
k′(t)=2(t-1-lnt),再令g(t)=t-1-lnt,g′(t)=1-$\frac{1}{t}=\frac{t-1}{t}<0$,可得
g(t)>g(1)=0,进而k(t)单调递增,可得k(t)<k(1)=0,
∴h(t)单调递增,由洛必达法则,$\underset{lim}{t→1}[\frac{(t+1)lnt}{t-1}-2]=\underset{lim}{t→1}[lnt+\frac{1}{t}+1-2]=0$,
∴h(t)>0,lnx1x2>0,则x1x2>1.
点评 本题考查利用导数研究函数的单调性,考查了利用导数求函数的极值,着重考查函数构造法,考查数学转化思想方法,题目设置难度较大.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
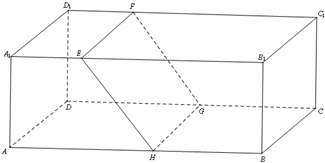 如图,在长方体ABCD-A1B1C1D1中,AB=16,AA1=8,BC=10,点E,F 分别在A1B1C1D1上,A1E=D1F=4,过点E,F的平面α与此长方体的面相交,交线围成一个正方形EFGH.
如图,在长方体ABCD-A1B1C1D1中,AB=16,AA1=8,BC=10,点E,F 分别在A1B1C1D1上,A1E=D1F=4,过点E,F的平面α与此长方体的面相交,交线围成一个正方形EFGH.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
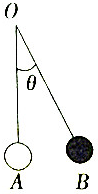 如图所示,一个单摆以OA为始边,OB为终边的角θ(-π<θ<π)与时间t(s)满足函数关系式θ=$\frac{1}{2}$sin(2t+$\frac{π}{2}$),则当t=0时,角θ的大小及单摆频率是( )
如图所示,一个单摆以OA为始边,OB为终边的角θ(-π<θ<π)与时间t(s)满足函数关系式θ=$\frac{1}{2}$sin(2t+$\frac{π}{2}$),则当t=0时,角θ的大小及单摆频率是( )| A. | $\frac{1}{2}$,$\frac{1}{π}$ | B. | 2,$\frac{1}{π}$ | C. | $\frac{1}{2}$,π | D. | 2,π |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 6人 | B. | 9人 | C. | 10人 | D. | 7人 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com