
分析 (1)求导,令f′(x)=0,根据函数单调性与导数的关系,即可求得函数f(x)的极值;
(2)采用分析法,要证明f(e+x)>f(e-x),只需证(e-x)ln(e+x)>(e+x)ln(e-x),构造辅助函数求导,由F′(x)>0,即可求得函数单调性递增,F(x)>F(0)=0,即可求得f(e+x)>f(e-x);
(3)由(1)可知0<x1<e<x2,则0<e-x1<e,由(2)可知,f(x)在(e,+∞)上单调递减,x1+x2>2e,x0=$\frac{{x}_{1}+{x}_{2}}{2}$>e,即可f'(x0)<0.
解答 解:(1)由f(x)=$\frac{lnx}{x}$,x>0,求导f′(x)=$\frac{1-lnx}{{x}^{2}}$,
当x∈(0,e),f′(x)>0,f(x)单调递增,
x∈(e,+∞)时,f′(x)<0,f(x)单调递减,
∴当x=e时,f(x)取极大值为$\frac{1}{e}$,无极小值,
(2)证明:要证明f(e+x)>f(e-x),即证$\frac{ln(e+x)}{e+x}$>$\frac{ln(e-x)}{e-x}$,
只需证(e-x)ln(e+x)>(e+x)ln(e-x),
设F(x)=(e-x)ln(e+x)-(e+x)ln(e-x),
求导F′(x)=$\frac{2({e}^{2}+{x}^{2})}{{e}^{2}-{x}^{2}}$-ln(e2-x2)=[2-ln(e2-x2)]+$\frac{4{x}^{2}}{{e}^{2}-{x}^{2}}$>0,
∴f(x)在(0,e)单调递增,
∴F(x)>F(0)=0,
∴(e-x)ln(e+x)>(e+x)ln(e-x),
∴f(e+x)>f(e-x),
(3)证明:不妨设x1<x2,由(1)可知0<x1<e<x2,
由0<e-x1<e,
由(2)可知:f[e+(e-x1)]>f[e-(e-x1)]=f(x1)=f(x2),
由2e-x1>e,x2>e,且f(x)在(e,+∞)上单调递减,
即x1+x2>2e,
则x0=$\frac{{x}_{1}+{x}_{2}}{2}$>e,
∴f'(x0)<0.
点评 本题考查导数的综合应用,考查导数与函数单调性及极值的关系,考查分析法证明不等式成立,考查计算能力,属于中档题.


 三点一测快乐周计划系列答案
三点一测快乐周计划系列答案科目:高中数学 来源: 题型:选择题
| ξ | -1 | 0 | 1 |
| P | $\frac{1}{3}$ | a | b |
| A. | $\frac{5}{6}$ | B. | $\frac{41}{48}$ | C. | 1 | D. | $\frac{2}{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $(-1,-\frac{1}{2})$ | B. | $(1,-\frac{1}{2})$ | C. | $(-\frac{1}{2},1)$ | D. | $(-\frac{1}{2},-1)$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
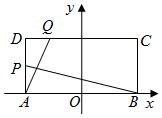 如图,在矩形ABCD中,|AB|=4,|AD|=2,O为AB中点,P,Q分别是AD和CD上的点,且满足①$\frac{|AP|}{|AD|}$=$\frac{|DQ|}{|DC|}$,②直线AQ与BP的交点在椭圆E:$\frac{x^2}{a^2}$+$\frac{y^2}{b^2}$=1(a>b>0)上.
如图,在矩形ABCD中,|AB|=4,|AD|=2,O为AB中点,P,Q分别是AD和CD上的点,且满足①$\frac{|AP|}{|AD|}$=$\frac{|DQ|}{|DC|}$,②直线AQ与BP的交点在椭圆E:$\frac{x^2}{a^2}$+$\frac{y^2}{b^2}$=1(a>b>0)上.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
 秦九韶是我国南宋时期的数学家,他在《数学九章》中提出的多项式的秦九韶算法,至今仍是比较先进的算法,如图是事项该算法的程序框图,执行该程序框图,若输入n,x的值分别为4,2,则输出v的值为( )
秦九韶是我国南宋时期的数学家,他在《数学九章》中提出的多项式的秦九韶算法,至今仍是比较先进的算法,如图是事项该算法的程序框图,执行该程序框图,若输入n,x的值分别为4,2,则输出v的值为( )| A. | 5 | B. | 12 | C. | 25 | D. | 50 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 贷款期限 | 6个月 | 12个月 | 18个月 | 24个月 | 36个月 |
| 频数 | 20 | 40 | 20 | 10 | 10 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 10 | B. | 11 | C. | 12 | D. | 13 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | {1} | B. | {0,1} | C. | [0,2) | D. | ∅ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com