若函数f(x)=$\frac{x}{ax+b}$=1.又方程f(x)=x有唯一解.则a+b=$\frac{3}{2}$．题目和参考答案——青夏教育精英家教网—

1．若函数f（x）=$\frac{x}{ax+b}$（a≠0），f（2）=1，又方程f（x）=x有唯一解，则a+b=$\frac{3}{2}$．

分析易知f（2）=$\frac{2}{2a+b}$=1，化简f（x）-x=$\frac{x（1-ax-b）}{ax+b}$，从而可得$\left\{\begin{array}{l}{2a+b=2}\\{1-b=0}\end{array}\right.$，从而解得．

解答解：由题意得，
f（2）=$\frac{2}{2a+b}$=1，
f（x）-x=$\frac{x}{ax+b}$-x=$\frac{x（1-ax-b）}{ax+b}$=0，
故$\left\{\begin{array}{l}{2a+b=2}\\{1-b=0}\end{array}\right.$，
解得，a=$\frac{1}{2}$，b=1；
故a+b=$\frac{3}{2}$；
故答案为：$\frac{3}{2}$．

点评本题考查了函数的化简与运算，属于中档题．

练习册系列答案

每日10分钟口算心算速算天天练系列答案

每时每刻快乐优加系列答案

孟建平培优一号系列答案

孟建平毕业总复习系列答案

年级	高中课程	年级	初中课程
高一	高一免费课程推荐！	初一	初一免费课程推荐！
高二	高二免费课程推荐！	初二	初二免费课程推荐！
高三	高三免费课程推荐！	初三	初三免费课程推荐！
更多初中、高中辅导课程推荐,点击进入>>

相关习题

科目：高中数学 来源： 题型：选择题

11．已知某几何体的三视图如图所示，则该几何体的表面积（　　）

A．

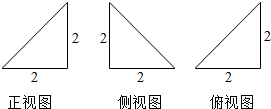
B．

$6+2\sqrt{3}$

C．

$8+8\sqrt{2}$

D．

$4+4\sqrt{2}$

查看答案和解析>>

科目：高中数学 来源： 题型：解答题

12．已知A，B（不与原点O重合）分别在圆C₁：（x-2）²+y²=4与圆C₂：（x-1）²+y²=1上，且OA⊥OB．
（1）若以原点为极点，x轴的正半轴为极轴建立极坐标系，当A的极角为$\frac{π}{3}$时，求A，B的极坐标；
（2）求|OA|•|OB|的最大值．

查看答案和解析>>

科目：高中数学 来源： 题型：解答题

9．

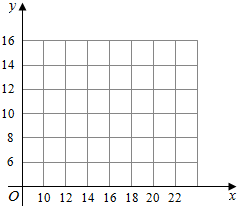每年七夕，琳琅满目的饰品在各大品牌店中成为年轻人亲眯的对象，这也使各大珠宝公司挖空心思，设计出匠心独运的饰品．某珠宝公司市场专员甲对该公司的一款项链的单价x（百元）和单位时间内的销售量y（件）之间的关系作出价格分析，所得数据如下：

单价x（百元）	a₁	a₂	a₃	a₄	a₅
单位时间内销售量y（件）	14	13	10	7	5

其中价格x（元）恰为公差为2的等差数列{a_n}的前5项，且等差数列{a_n}的前10项和为230．
（1）请根据上述数据在下列网格纸中绘制散点图；
（2）请根据表格数据计算项链的单价x（百元）和单位时间内的销售量y（件）之间的回归直线方程．
$\left\{\begin{array}{l}{\stackrel{∧}{b}=\frac{\sum_{i=1}^{n}{x}_{i}{y}_{i}-n\overline{x}•\overline{y}}{\sum_{i=1}^{n}{{x}_{i}}^{2}-n{\overline{x}}^{2}}=\frac{\sum_{i=1}^{n}（{x}_{i}-\overline{x}）（{y}_{i}-\overline{y}）}{\sum_{i=1}^{n}（{x}_{i}-\overline{x}）^{2}}}\\{\stackrel{∧}{a}=\overline{y}-\stackrel{∧}{b}\overline{x}}\end{array}\right.$．

查看答案和解析>>

科目：高中数学 来源： 题型：选择题

16．已知函数f（x）=（sinx-cosx）sinx，x∈R，则f（x）的最小正周期是（　　）

A．

B．

2π

C．

$\frac{π}{2}$

D．

查看答案和解析>>

科目：高中数学 来源： 题型：解答题

6．当n＞2时，证明：3ⁿ＞（n+2）•2^n-1．