
| A. | (-$\frac{1}{60}$,0) | B. | (0,$\frac{15}{4}$) | C. | (0,-$\frac{15}{4}$) | D. | ($\frac{1}{60}$,0) |
分析 根据三角形的角平分线定理求得丨BD丨及丨DC丨根据向量的共线定理求得$\overrightarrow{AD}$=$\frac{5}{9}$$\overrightarrow{AB}$+$\frac{4}{9}$$\overrightarrow{AC}$,由I为△ABC的内心,$\frac{丨AC丨}{丨CD丨}$=$\frac{丨AI丨}{丨ID丨}$=$\frac{3}{2}$,丨AI丨=$\frac{3}{5}$丨AD丨,即可求得m和n的值,根据抛物线的性质即可求得抛物线的焦点坐标.
解答 解:AI的延长线交BC于D,由三角形的角平分线定理,$\frac{丨AB丨}{丨AC丨}$=$\frac{丨BD丨}{丨DC丨}$,
∴丨BD丨=$\frac{8}{3}$,丨DC丨=$\frac{10}{3}$,$\overrightarrow{BD}$=$\frac{4}{9}$$\overrightarrow{BC}$=$\frac{4}{9}$($\overrightarrow{AC}$-$\overrightarrow{AB}$),
$\overrightarrow{AD}$=$\overrightarrow{AB}$+$\overrightarrow{BD}$=$\overrightarrow{AB}$+$\frac{4}{9}$($\overrightarrow{AC}$-$\overrightarrow{AB}$)=$\frac{5}{9}$$\overrightarrow{AB}$+$\frac{4}{9}$$\overrightarrow{AC}$,
由I为△ABC的内心,则$\frac{丨AC丨}{丨CD丨}$=$\frac{丨AI丨}{丨ID丨}$=$\frac{5}{\frac{10}{3}}$=$\frac{3}{2}$,
则丨AI丨=$\frac{3}{5}$丨AD丨,
∴$\overrightarrow{AI}$=$\frac{1}{3}$$\overrightarrow{AB}$+$\frac{4}{15}$$\overrightarrow{AC}$,
∴m=$\frac{1}{3}$,n=$\frac{4}{15}$,
则m-n=$\frac{1}{3}$-$\frac{4}{15}$=$\frac{1}{15}$,
∴曲线方程x2=15y,则抛物线的焦点坐标为(0,$\frac{15}{4}$),
故选B.
点评 本题考查向量的共线的应用,考查向量的线性运算,考查三角形的三角形的角平分线定理,三角形内心的性质,考查抛物线的焦点坐标的求法,考查计算能力,属于中档题.


 阳光同学一线名师全优好卷系列答案
阳光同学一线名师全优好卷系列答案科目:高中数学 来源: 题型:选择题
| A. | f($\frac{π}{6}$)>$\sqrt{2}$f($\frac{π}{4}$) | B. | $\sqrt{2}$sin1•f(1)>f($\frac{π}{4}$) | C. | f($\frac{π}{6}$)>$\sqrt{3}$f($\frac{π}{3}$) | D. | $\sqrt{2}$f($\frac{π}{4}$)>$\sqrt{3}$f($\frac{π}{3}$) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 40 | B. | 60 | C. | 80 | D. | 100 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
 为了解甲、乙两厂产品的质量,从甲厂生产的产品中随机抽取3件样品,从乙厂生产的产品中随机抽取4件样品,测量产品中某种元素的含量(单位:毫克),如图是测量数据的茎叶图.若它们的中位数相同,平均数也相同,则图中的m,n的比值$\frac{m}{n}$=( )
为了解甲、乙两厂产品的质量,从甲厂生产的产品中随机抽取3件样品,从乙厂生产的产品中随机抽取4件样品,测量产品中某种元素的含量(单位:毫克),如图是测量数据的茎叶图.若它们的中位数相同,平均数也相同,则图中的m,n的比值$\frac{m}{n}$=( )| A. | 1 | B. | $\frac{1}{3}$ | C. | $\frac{8}{3}$ | D. | $\frac{3}{8}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
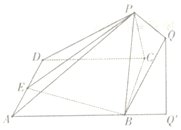 已知如图所示的几何体中,四边形ABCD是边长为2的菱形,面PBC⊥面A BCD,点E是AD 的中点,PQ∥面ABCD且点Q在面ABCD上的射影Q′落在AB的延长线上,若PQ=1,PB=$\sqrt{2}$,且($\overrightarrow{PB}+\overrightarrow{PC}$)•$\overrightarrow{BC}$=0,$\overrightarrow{AB}•\overrightarrow{AD}$=2
已知如图所示的几何体中,四边形ABCD是边长为2的菱形,面PBC⊥面A BCD,点E是AD 的中点,PQ∥面ABCD且点Q在面ABCD上的射影Q′落在AB的延长线上,若PQ=1,PB=$\sqrt{2}$,且($\overrightarrow{PB}+\overrightarrow{PC}$)•$\overrightarrow{BC}$=0,$\overrightarrow{AB}•\overrightarrow{AD}$=2查看答案和解析>>
科目:高中数学 来源: 题型:解答题
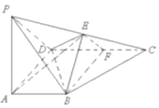 如图,在四棱锥P-ABCD中,PA⊥面ABCD,AB∥CD,CD⊥AD,AD=CD=2AB=2,E,F分别为PC,CD的中点
如图,在四棱锥P-ABCD中,PA⊥面ABCD,AB∥CD,CD⊥AD,AD=CD=2AB=2,E,F分别为PC,CD的中点查看答案和解析>>
科目:高中数学 来源: 题型:解答题
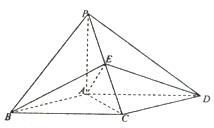 如图,在四棱锥P-ABCD中,底面ABCD为平行四边形,AP=AB=AC=a,AD=$\sqrt{2}$a,PA⊥底面ABCD.
如图,在四棱锥P-ABCD中,底面ABCD为平行四边形,AP=AB=AC=a,AD=$\sqrt{2}$a,PA⊥底面ABCD.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 原点轴对称 | B. | x轴对称 | C. | y轴对称 | D. | y=x对 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com