
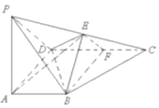
 如图,在四棱锥P-ABCD中,PA⊥面ABCD,AB∥CD,CD⊥AD,AD=CD=2AB=2,E,F分别为PC,CD的中点
如图,在四棱锥P-ABCD中,PA⊥面ABCD,AB∥CD,CD⊥AD,AD=CD=2AB=2,E,F分别为PC,CD的中点分析 (1)建立坐标系,设PA=a,求出各向量的坐标,利用数量积证明AB⊥BF,AB⊥BE,故而AB⊥平面BEF,于是平面ABE⊥平面BEF;
(2)求出两平面的法向量,计算法向量的夹角,根据二面角的范围列不等式组解出a的范围.
解答 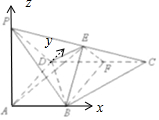 (1)证明:以A为原点,以AB,AD,AP为坐标轴建立空间直角坐标系,设PA=a,
(1)证明:以A为原点,以AB,AD,AP为坐标轴建立空间直角坐标系,设PA=a,
则A(0,0,0),B(1,0,0),F(1,2,0,),E(1,1,$\frac{a}{2}$),
∴$\overrightarrow{AB}$=(1,0,0),$\overrightarrow{BE}$=(0,1,$\frac{a}{2}$),$\overrightarrow{BF}$=(0,2,0),
∴$\overrightarrow{AB}•\overrightarrow{BE}$=0,$\overrightarrow{AB}•\overrightarrow{BF}$=0,
∴AB⊥BE,AB⊥BF,又BE∩BF=B,
AB⊥平面BEF,又AB?平面ABE,
∴平面ABE⊥平面BEF.
(2)解:由(1)知$\overrightarrow{BD}$=(-1,2,0),$\overrightarrow{BE}$=(0,1,$\frac{a}{2}$),
设平面BDE的法向量为$\overrightarrow{n}$=(x,y,z),则$\left\{\begin{array}{l}{\overrightarrow{n}•\overrightarrow{BD}=0}\\{\overrightarrow{n}•\overrightarrow{BE}=0}\end{array}\right.$,
∴$\left\{\begin{array}{l}{-x+2y=0}\\{y+\frac{a}{2}z=0}\end{array}\right.$,令z=1得$\overrightarrow{n}$=(-a,-$\frac{a}{2}$,1),
∵PA⊥平面ABCD,∴$\overrightarrow{m}$=(0,0,1)是平面ABCD的一个法向量,
∴cos<$\overrightarrow{m},\overrightarrow{n}$>=$\frac{\overrightarrow{m}•\overrightarrow{n}}{|\overrightarrow{m}||\overrightarrow{n}|}$=$\frac{1}{1×\sqrt{\frac{{5a}^{2}}{4}+1}}$,
∵平面EBD与平面ABCD所成锐二面角θ∈[$\frac{π}{4}$,$\frac{π}{3}$],
∴$\frac{1}{2}$≤$\frac{1}{1×\sqrt{\frac{{5a}^{2}}{4}+1}}$≤$\frac{\sqrt{2}}{2}$,
解得:$\frac{2\sqrt{5}}{5}$≤a≤$\frac{2\sqrt{15}}{5}$.
点评 本题考查了面面垂直的判定,空间向量与二面积的计算,属于中档题.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:选择题
| A. | θ=$\frac{π}{12}$,t的最小值为$\frac{π}{12}$ | B. | θ=$\frac{π}{12}$,t的最小值为$\frac{π}{6}$ | ||
| C. | θ=$\frac{π}{6}$,t的最小值为$\frac{π}{6}$ | D. | θ=$\frac{π}{6}$,t的最小值为$\frac{π}{12}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\sqrt{2}$ | B. | $\frac{{3\sqrt{3}}}{2}$ | C. | $\frac{{3\sqrt{2}}}{2}$ | D. | $\sqrt{5}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (-$\frac{1}{60}$,0) | B. | (0,$\frac{15}{4}$) | C. | (0,-$\frac{15}{4}$) | D. | ($\frac{1}{60}$,0) |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
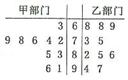 渝州集团对所有员工进行了职业技能测试从甲、乙两部门中各任选10名员工的测试成绩(单位:分)数据的茎叶图如图所示.
渝州集团对所有员工进行了职业技能测试从甲、乙两部门中各任选10名员工的测试成绩(单位:分)数据的茎叶图如图所示.| 分数 | [60,70) | [70,80) | [80,90) | [90,100] |
| 奖金 | a | 2a | 3a | 4a |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 是奇函数 | B. | 在区间$(\frac{π}{12},\frac{7π}{12})$上单调递增 | ||
| C. | $(-\frac{π}{12},0)$为其图象的一个对称中心 | D. | 最小正周期为π |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{6}$ | B. | $\frac{1}{3}$ | C. | $\frac{1}{2}$ | D. | $\frac{5}{6}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com