
| A. | 是奇函数 | B. | 在区间$(\frac{π}{12},\frac{7π}{12})$上单调递增 | ||
| C. | $(-\frac{π}{12},0)$为其图象的一个对称中心 | D. | 最小正周期为π |
分析 判断函数的周期,求出对称中心,函数的单调性,判断选项即可.
解答 解:函数y=tan(2x+$\frac{2π}{3}$),函数的周期为:$\frac{π}{2}$,
当x=0时,y=-$\sqrt{3}$,函数不是奇函数;
因为kπ$-\frac{π}{2}$$<2x+\frac{2π}{3}$$<kπ+\frac{π}{2}$,k∈Z,解得x∈($\frac{kπ}{2}-\frac{7π}{12}$,$\frac{kπ}{2}-\frac{π}{12}$),k∈Z,
所以在区间$(\frac{π}{12},\frac{7π}{12})$上单调递增,不正确;
x=-$\frac{π}{12}$时,y=tan($\frac{π}{2}$)不存在,所以$(-\frac{π}{12},0)$为其图象的一个对称中心.正确.
故选:C.
点评 本题考查命题的真假的判断,正切函数的单调性、奇偶性、对称性、周期性的求法,考查计算能力.


科目:高中数学 来源: 题型:选择题
 为了解甲、乙两厂产品的质量,从甲厂生产的产品中随机抽取3件样品,从乙厂生产的产品中随机抽取4件样品,测量产品中某种元素的含量(单位:毫克),如图是测量数据的茎叶图.若它们的中位数相同,平均数也相同,则图中的m,n的比值$\frac{m}{n}$=( )
为了解甲、乙两厂产品的质量,从甲厂生产的产品中随机抽取3件样品,从乙厂生产的产品中随机抽取4件样品,测量产品中某种元素的含量(单位:毫克),如图是测量数据的茎叶图.若它们的中位数相同,平均数也相同,则图中的m,n的比值$\frac{m}{n}$=( )| A. | 1 | B. | $\frac{1}{3}$ | C. | $\frac{8}{3}$ | D. | $\frac{3}{8}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
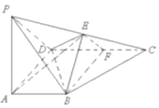 如图,在四棱锥P-ABCD中,PA⊥面ABCD,AB∥CD,CD⊥AD,AD=CD=2AB=2,E,F分别为PC,CD的中点
如图,在四棱锥P-ABCD中,PA⊥面ABCD,AB∥CD,CD⊥AD,AD=CD=2AB=2,E,F分别为PC,CD的中点查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
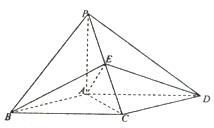 如图,在四棱锥P-ABCD中,底面ABCD为平行四边形,AP=AB=AC=a,AD=$\sqrt{2}$a,PA⊥底面ABCD.
如图,在四棱锥P-ABCD中,底面ABCD为平行四边形,AP=AB=AC=a,AD=$\sqrt{2}$a,PA⊥底面ABCD.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 人数 x y | A | B | C |
| A | 14 | 40 | 10 |
| B | a | 36 | b |
| C | 28 | 8 | 34 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com