
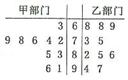
 渝州集团对所有员工进行了职业技能测试从甲、乙两部门中各任选10名员工的测试成绩(单位:分)数据的茎叶图如图所示.
渝州集团对所有员工进行了职业技能测试从甲、乙两部门中各任选10名员工的测试成绩(单位:分)数据的茎叶图如图所示.| 分数 | [60,70) | [70,80) | [80,90) | [90,100] |
| 奖金 | a | 2a | 3a | 4a |
分析 (1)利用古典概型的概率公式求解即可.
(2)求出ξ的可能取值为ξ=0,1,2,3;求出概率,得到分布列,然后求解期望即可.
解答 解:(1)20名员工中85(分)以上有5人,${p_1}=\frac{{C_5^2•C_{15}^1}}{{C_{20}^3}}=\frac{5}{38}$;
(2)甲部门中任选一人绩效工资不低于3a的概率为$\frac{2}{5}$,
所以ξ的可能取值为ξ=0,1,2,3;
$P({ξ=0})=C_3^0{({\frac{3}{5}})^3}=\frac{27}{125}$;$P({ξ=1})=C_3^1{({\frac{2}{5}})^1}•{({\frac{3}{5}})^2}=\frac{54}{125}$;$P({ξ=2})=C_3^2{({\frac{2}{5}})^2}•{({\frac{3}{5}})^1}=\frac{36}{125}$;$P({ξ=3})=C_3^3{({\frac{2}{5}})^3}=\frac{8}{125}$,
ξ的分布列为:
| ξ | 0 | 1 | 2 | 3 |
| P | $\frac{27}{125}$ | $\frac{54}{125}$ | $\frac{36}{125}$ | $\frac{8}{125}$ |
点评 本题考查离散性随机变量的分布列以及期望的求法,考查分析问题解决问题的能力.


科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{4}$ | B. | $\frac{1}{3}$ | C. | $\frac{1}{2}$ | D. | $\frac{2}{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 40 | B. | 60 | C. | 80 | D. | 100 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
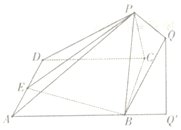 已知如图所示的几何体中,四边形ABCD是边长为2的菱形,面PBC⊥面A BCD,点E是AD 的中点,PQ∥面ABCD且点Q在面ABCD上的射影Q′落在AB的延长线上,若PQ=1,PB=$\sqrt{2}$,且($\overrightarrow{PB}+\overrightarrow{PC}$)•$\overrightarrow{BC}$=0,$\overrightarrow{AB}•\overrightarrow{AD}$=2
已知如图所示的几何体中,四边形ABCD是边长为2的菱形,面PBC⊥面A BCD,点E是AD 的中点,PQ∥面ABCD且点Q在面ABCD上的射影Q′落在AB的延长线上,若PQ=1,PB=$\sqrt{2}$,且($\overrightarrow{PB}+\overrightarrow{PC}$)•$\overrightarrow{BC}$=0,$\overrightarrow{AB}•\overrightarrow{AD}$=2查看答案和解析>>
科目:高中数学 来源: 题型:解答题
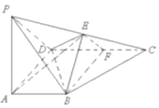 如图,在四棱锥P-ABCD中,PA⊥面ABCD,AB∥CD,CD⊥AD,AD=CD=2AB=2,E,F分别为PC,CD的中点
如图,在四棱锥P-ABCD中,PA⊥面ABCD,AB∥CD,CD⊥AD,AD=CD=2AB=2,E,F分别为PC,CD的中点查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图,在多面体ABCDEF中,正三角形BCE所在平面与菱形ABCD所在的平面垂直,FD⊥平面ABCD,且$BC=4,FD=2\sqrt{3}$.
如图,在多面体ABCDEF中,正三角形BCE所在平面与菱形ABCD所在的平面垂直,FD⊥平面ABCD,且$BC=4,FD=2\sqrt{3}$.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
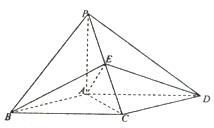 如图,在四棱锥P-ABCD中,底面ABCD为平行四边形,AP=AB=AC=a,AD=$\sqrt{2}$a,PA⊥底面ABCD.
如图,在四棱锥P-ABCD中,底面ABCD为平行四边形,AP=AB=AC=a,AD=$\sqrt{2}$a,PA⊥底面ABCD.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (-2,-1) | B. | (-1,0) | C. | (0,1) | D. | (1,2) |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com